String matching

Searching for a pattern is a fundamental problem when dealing with text

• Editing a document
• Answering an internet search query
• Looking for a match in a gene sequence

Example

• an occurs in banana at two positions

Formally

• A text string t of length n A pattern string p of length m
• Both t and p are drawn from an alphabet of valid letters, denoted Σ
• Find every position i in t such that t[i:i+m] == p

Brute force approach

Nested scan from left to right in t

def stringmatch(t,p):
    poslist = []
    for i in range(len(t)-len(p)+1):
        matched = True
        j = 0
        while j < len(p) and matched:
            if t[i+j] != p[j]:
                matched = False
            j = j+1
        if matched:
            poslist.append(i)
    return(poslist)
print(stringmatch('abababbababbbbababab','abab'))

Output

[0, 2, 7, 14, 16]

Complexity

$O(nm)$

 

Nested scan from right to left

def stringmatchrev(t,p):
    poslist = []
    for i in range(len(t)-len(p)+1):
        matched = True
        j = len(p)-1
        while j >= 0 and matched:
            if t[i+j] != p[j]:
                matched = False
            j = j-1
        if matched:
            poslist.append(i)
    return(poslist)
print(stringmatchrev('abababbababbbbababab','abab'))

Output

[0, 2, 7, 14, 16]

Complexity

$O(nm)$

 

Speeding up the brute force algorithm

• Text t, pattern p of of lengths n, m

• For each starting position i in t, compare t[i:i+m] with p

  • Scan t[i:i+m] right to left

• While matching, we find a letter in t that does not appear in p

  • t = bananamania, p = bulk

• Shift the next scan to position after mismatched letter

• What if the mismatched letter does appear in p?

 

Boyer-Moore Algorithm

Algorithm

• Initialize last[c] for each c in p

  • Single scan, rightmost value is recorded

• Nested loop, compare each segment t[i:i+len(p)] with p

• If p matches, record and shift by 1

• We find a mismatch at t[i+j]

  • If j > last[t[i+j]], shift by j - last[t[i+j]]

  • If last[t[i+j]] > j, shift by 1

    • Should not shift p to left!

  • If t[i+j] not in p, shift by j+1

Implementation

def boyermoore(t,p):
    last = {} # Preprocess
    for i in range(len(p)):
        last[p[i]] = i
    poslist=[]
    i = 0
    while i <= (len(t)-len(p)):
        matched,j = True,len(p)-1
        while j >= 0 and matched:
            if t[i+j] != p[j]:
                matched = False
            j = j - 1
        if matched:
            poslist.append(i)
            i = i + 1
        else:
            j = j + 1
            if t[i+j] in last.keys():
                i = i + max(j-last[t[i+j]],1)
            else:
                i = i + j + 1
    return(poslist)
print(boyermoore('abcaaacabc','abc'))

Output

[0, 7]

Complexity

Worst case remains $O(nm)$

If t = aaa...a, p = baaa

 

Rabin-Karp Algorithm

• Suppose Σ = {0, 1, . . . , 9}
• Any string over Σ can be thought of as a number in base 10
• Pattern $p$ is an $m$-digit number $n_p$
• Each substring of length $m$ in the text $t$ is again an $m$-digit number
• Scan $t$ and compare the number $n_b$ generated by each block of $m$ letters with the pattern number $n_p$

Implementation

def rabinkarp(t,p):
    poslist = []
    numt,nump = 0,0
    for i in range(len(p)):
        numt = 10*numt + int(t[i])
        nump = 10*nump + int(p[i])
    if numt == nump:
        poslist.append(0)
    for i in range(1,len(t)-len(p)+1):
        numt = numt - int(t[i-1])*(10**(len(p)-1))
        numt = 10*numt + int(t[i+len(p)-1])
        if numt == nump:
            poslist.append(i)
    return(poslist)
print(rabinkarp('233323233454323','23'))

Output

[0, 4, 6, 13]

Analysis

• Preprocessing time is $O(m)$

  • To convert t[0:m], p to numbers

• Worst case for general alphabets is $O(nm)$

  • Every block t[i:i+m] may have same remainder modulo q as the pattern p
  • Must validate each block explicitly, like brute force

• In practice number of spurious matches will be small

• If |Σ| is small enough to not require modulo arithmetic, overall time is $O(n + m)$, or $O(n)$, since $m << n$

  • Also if we can choose q carefully to ensure $O(1)$ spurious matches

 

Rabin Karp Implementation for strings

def rabin_karp(text, pattern):
    match_found =[]
    n = len(text)
    m = len(pattern)    
    # Prime number to use for the hash function
    prime = 101   
    # Calculate the hash value of the pattern
    pattern_hash = 0
    for i in range(m):
        pattern_hash += ord(pattern[i])
    pattern_hash = pattern_hash % prime
    
    # Calculate the hash value of the first substring of the text
    text_hash = 0
    for i in range(m):
        text_hash += ord(text[i])
    text_hash = text_hash % prime
    # Iterate through the text, checking for matches with the pattern
    for i in range(n - m + 1):
        # Check if the current substring matches the pattern
        if text_hash == pattern_hash and text[i:i+m] == pattern:
            match_found.append(i)       
        # Calculate the hash value of the next substring
        if i < n - m:
            text_hash = (text_hash - ord(text[i]) + ord(text[i+m]))
            text_hash = text_hash % prime
    # No match found
    return match_found
text = 'abcdbabcdb'
pattern = 'abcdb'
print(rabin_karp(text, pattern))

Output

[0, 5]

 

 

Knuth-Morris-Pratt algorithm

• Compute the automaton for p efficiently

• Match p against itself

  • match[j] = kif suffix of p[:j+1] matches prefix p[:k]

• Suppose suffix of p[:j+1] matches prefix p[:k]

  • If p[j+1] == p[k], extend the match
  • Otherwise try to find a shorter prefix that can be extended by p[j+1]

• Usually refer to match as failure function fail

  • Where to fall back if match fails

Computing the fail function

• Initialize fail[j] = 0 for all j

• k keeps track of length of current match

• j is next position to update fail

• If p[j] == p[k] extend the match, set fail[j] = k+1

• If p[j] != p[k] find a shorter prefix that matches suffix of p[:j]

  • Step back to fail[k-1]

• If we don’t find a nontrivial prefix to extend, retain fail[j] = 0, move to next position

Implementation of fail function

def kmp_fail(p):
    m = len(p)
    fail = [0 for i in range(m)]
    j,k = 1,0
    while j < m:
        if p[j] == p[k]:
            fail[j] = k+1
            j,k = j+1,k+1
        elif k > 0:
            k = fail[k-1]
        else:
            j = j+1
    return(fail)
print(kmp_fail('abcaabca'))

Output

[0, 0, 0, 1, 1, 2, 3, 4]

Complexity

$O(n)$

 

Implementation of KMP algorithm

• Scan t from beginning
• j is next position in t
• k is currently matched position in p
• If t[j] == p[k] extend the match
• If t[j] != p[k], update match prefix
• If we reach the end of the while loop, no match

def kmp_fail(p):
    m = len(p)
    fail = [0 for i in range(m)]
    j,k = 1,0
    while j < m:
        if p[j] == p[k]:
            fail[j] = k+1
            j,k = j+1,k+1
        elif k > 0:
            k = fail[k-1]
        else:
            j = j+1
    return(fail)

def find_kmp(t, p):
    match =[]
    n,m = len(t),len(p)
    if m == 0:
        match.append(0)
    fail = kmp_fail(p)
    j = 0
    k = 0
    while j < n:
        if t[j] == p[k]:
            if k == m - 1:
                match.append(j - m + 1)
                k = 0
                j = j - m + 2
            else:
                j,k = j+1,k+1
        elif k > 0:
            k = fail[k-1]
        else:
            j = j+1
    return(match)
print(find_kmp('ababaabbaba','aba'))

Output

[0, 2, 8]

Analysis

• The Knuth, Morris, Pratt algorithm efficiently computes the automaton describing prefix matches in the pattern p
• Complexity of preprocessing the fail function is $O(m)$
• After preprocessing, can check matches in the text t in $O(n)$
• Overall, KMP algorithm works in time $O(m + n)$

 

Tries

• A trie is a special kind of tree

  • From “information retrieval”
  • Pronounced try, distinguish from tree

• Rooted tree

  • Other than root, each node labelled by a letter from Σ
  • Children of a node have distinct labels

• Each maximal path is a word

  • One word should not be a prefix of another
  • Add special end of word symbol $

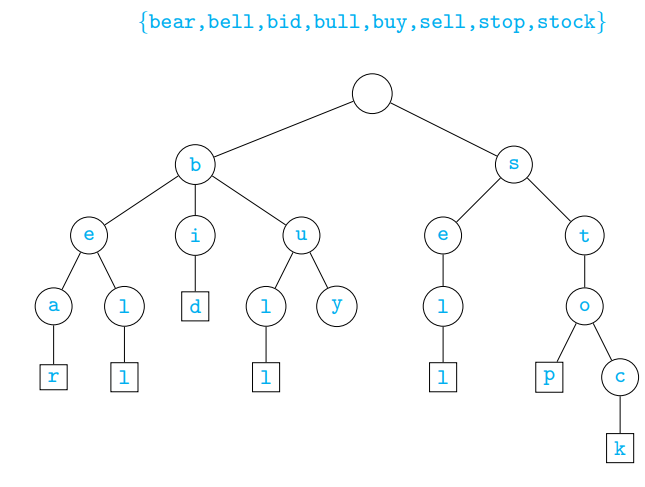
• Build a trie T from a set of words S with s words and n total symbols

• To search for a word w, follow its path

  • If the node we reach has $ as a successor represent $w\in S$
  • $w\not\in S-$ if path cannot be completed, or w is a prefix of some $w^`\in S$

• Build a trie T from a set of words S with s words and n total symbols

• Basic properties for T built from S

  • Height of T is $max_{w∈S} len(w)$
  • A node has at most |Σ| children
  • The number of leaves in T is s
  • The number of nodes in T is n + 1, plus s nodes labelled $

Implementation of Tries

class Trie:
    def __init__(self,S=[]):
        self.root = {}
        for s in S:
            self.add(s)
    def add(self,s):
        curr = self.root
        s = s + "$"
        for c in s:
            if c not in curr.keys():
                curr[c] = {}
            curr = curr[c]
    def query(self,s):
        curr = self.root
        for c in s:
            if c not in curr.keys():
                return(False)
            curr = curr[c]
        if "$" in curr.keys():
            return(True)
        else:
            return(False)
        
T = Trie()
T.add('car')
T.add('card')
T.add('care')
T.add('dog')
T.add('done')
print(T.query('dog'))
print(T.query('cat'))

Output

True
False

Analysis

• Tries are useful to preprocess fixed text for multiple searches
• Searching for p is proportional to length of p
• Main drawback of a trie is size

 

Suffix Tries

• Expand S to include all suffixes

  • For simplicity, assume S = {s}
  • suffix(S) = {w | ∃v, vw = s}

• Build a trie for suffix(S)

  • Use $ to mark end of word
  • Suffix trie for S

• Using a suffix trie we can answer the following

  • Is w a substring of s?
  • How many times does w occur as a substring in s ?
  • What is the longest repeated substring in s ?

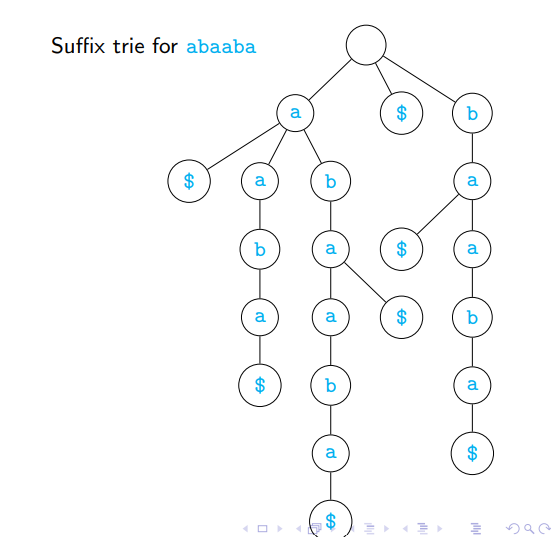
Implementation of suffix tries

class SuffixTrie:
    def __init__(self,s):
        self.root = {}
        s = s + "$"
        for i in range(len(s)):
            curr = self.root
            for c in s[i:]:
                if c not in curr.keys():
                    curr[c] = {}
                curr = curr[c]
    def followPath(self,s):
        curr = self.root
        for c in s:
            if c not in curr.keys():
                return(None)
            curr = curr[c]
        return(curr)
    def hasSuffix(self,s):
        node = self.followPath(s)
        return(node is not None and "$" in node.keys())
ST = SuffixTrie('card')
print(ST.root)
print(ST.followPath('a'))
print(ST.hasSuffix('aa'))

Output

{'r': {'d': {'$': {}}}}
False