Union-Find Data Structure

• A set S partitioned into components {C1, C2, . . . , Ck }

  • Each s ∈ S belongs to exactly one Cj

• Support the following operations

  • MakeUnionFind(S) — set up initial singleton components {s}, for each s ∈ S
  • Find(s) — return the component containing s
  • Union(s,s’) — merges components containing s, s 0

Visualization

Open Visualization

https://visualgo.net/en/ufds

Naïve Implementation of Union-Find

class MakeUnionFind:
    def __init__(self):
        self.components = {}
        self.size = 0
    def make_union_find(self,vertices):
        self.size = vertices
        for vertex in range(vertices):
            self.components[vertex] = vertex
    def find(self,vertex):
        return self.components[vertex]
    def union(self,u,v):
        c_old = self.components[u]
        c_new = self.components[v]
        for k in range(self.size):
            if self.components[k] == c_old:
                self.components[k] = c_new

Complexity

• MakeUnionFind(S) — $O(n)$
• Find(i) — $O(1)$
• Union(i,j) — $O(n)$
• Sequence of m Union() operations takes time $O(mn)$

Improved Implementation of Union-Find

class MakeUnionFind:
    def __init__(self):
        self.components = {}
        self.members = {}
        self.size = {}
    def make_union_find(self,vertices):
        for vertex in range(vertices):
            self.components[vertex] = vertex
            self.members[vertex] = [vertex]
            self.size[vertex] = 1
    def find(self,vertex):
        return self.components[vertex]
    def union(self,u,v):
        c_old = self.components[u]
        c_new = self.components[v]
        # Always add member in components which have greater size
        if self.size[c_new] >= self.size[c_old]:            
            for x in self.members[c_old]:
                self.components[x] = c_new
                self.members[c_new].append(x)
                self.size[c_new] += 1
        else:
            for x in self.members[c_new]:
                self.components[x] = c_old
                self.members[c_old].append(x)
                self.size[c_old] += 1

Complexity

• MakeUnionFind(S) — $O(n)$
• Find(i) — $O(1)$
• Union(i,j) — $O(logn)$

 

Improved Kruskal's algorithm using Union-find

class MakeUnionFind:
    def __init__(self):
        self.components = {}
        self.members = {}
        self.size = {}
    def make_union_find(self,vertices):
        for vertex in range(vertices):
            self.components[vertex] = vertex
            self.members[vertex] = [vertex]
            self.size[vertex] = 1
    def find(self,vertex):
        return self.components[vertex]
    def union(self,u,v):
        c_old = self.components[u]
        c_new = self.components[v]
        # Always add member in components which have greater size
        if self.size[c_new] >= self.size[c_old]:            
            for x in self.members[c_old]:
                self.components[x] = c_new
                self.members[c_new].append(x)
                self.size[c_new] += 1
        else:
            for x in self.members[c_new]:
                self.components[x] = c_old
                self.members[c_old].append(x)
                self.size[c_old] += 1


def kruskal(WList):
    (edges,TE) = ([],[])
    for u in WList.keys():
        edges.extend([(d,u,v) for (v,d) in WList[u]])
    edges.sort()
    mf = MakeUnionFind()
    mf.make_union_find(len(WList))
    for (d,u,v) in edges:
        if mf.components[u] != mf.components[v]:
            mf.union(u,v)
            TE.append((u,v,d))
        # We can stop the process if the size becomes equal to the total number of vertices
        # Which represent that a spanning tree is completed
        if mf.size[mf.components[u]]>= mf.size[mf.components[v]]:
            if mf.size[mf.components[u]] == len(WList):
                break
        else:
            if mf.size[mf.components[v]] == len(WList):
                break
    return(TE)

# Testcase

edge = [(0,1,10),(0,2,18),(0,3,6),(0,4,20),(0,5,13),(1,2,10),(1,3,10),(1,4,5),(1,5,7),(2,3,2),(2,4,14),(2,5,15),(3,4,17),(3,5,12),(4,5,10)]

size = 6
WL = {}
for i in range(size):
    WL[i] = []
for (i,j,d) in edge:
    WL[i].append((j,d))
print(kruskal(WL))

Output

[(2, 3, 2), (1, 4, 5), (0, 3, 6), (1, 5, 7), (0, 1, 10)]

Complexity

• Tree has $n − 1$ edges, so $O(n)$ Union() operations

• $O(n log n)$ amortized cost, overall

• Sorting E takes $O(m log m)$

  • Equivalently $O(m log n)$, since $m ≤ n^2$

• Overall time, $O((m + n) log n)$

 

Priority Queue

Need to maintain a collection of items with priorities to optimize the following operations

• delete max()

  • Identify and remove item with highest priority
  • Need not be unique

• insert()

  • Add a new item to the list

Heap

Binary tree

A binary tree is a tree data structure in which each node can contain at most 2 children, which are referred to as the left child and the right child.

Heap

Heap is a binary tree, filled level by level, left to right. There are two types of the heap:

• Max heap - For each node V in heap except for leaf nodes, the value of V should be greater or equal to its child's node value.
• Min heap - For each node V in heap except for leaf nodes, the value of V should be less or equal to its child's node value.

We can represent heap using array(list in python)

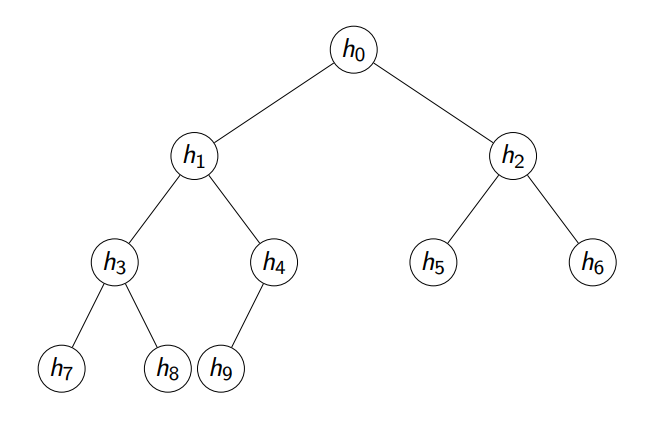
H = [h0, h1, h2, h3, h4, h5, h6, h7, h8, h9]

left child of H[i] = H[2 * i + 1]

Right child of H[i] = H[2 * i + 2]

Parent of H[i] = H[(i-1) // 2], for i > 0

 

Visualization

Open Visualization

https://visualgo.net/en/heap

Implementation of Maxheap

class maxheap:
    def __init__(self):
        self.A = []
    def max_heapify(self,k):
        l = 2 * k + 1
        r = 2 * k + 2
        largest = k
        if l < len(self.A) and self.A[l] > self.A[largest]:
            largest = l
        if r < len(self.A) and self.A[r] > self.A[largest]:
            largest = r
        if largest != k:
            self.A[k], self.A[largest] = self.A[largest], self.A[k]
            self.max_heapify(largest)

    def build_max_heap(self,L):
        self.A = []
        for i in L:
            self.A.append(i)
        n = int((len(self.A)//2)-1)
        for k in range(n, -1, -1):
            self.max_heapify(k)

        
    def delete_max(self):
        item = None
        if self.A != []:
            self.A[0],self.A[-1] = self.A[-1],self.A[0]
            item = self.A.pop()
            self.max_heapify(0)
        return item


    def insert_in_maxheap(self,d):
        self.A.append(d)
        index = len(self.A)-1
        while index > 0:
            parent = (index-1)//2
            if self.A[index] > self.A[parent]:
                self.A[index],self.A[parent] = self.A[parent],self.A[index]
                index = parent
            else:
                break

heap = maxheap()
heap.build_max_heap([1,2,3,4,5,6])
print(heap.A)
heap.insert_in_maxheap(7)
print(heap.A)
heap.insert_in_maxheap(8)
print(heap.A)
print(heap.delete_max())
print(heap.delete_max())
print(heap.A)

Output

[6, 5, 3, 4, 2, 1]
[7, 5, 6, 4, 2, 1, 3]
[8, 7, 6, 5, 2, 1, 3, 4]
8
7
[6, 5, 3, 4, 2, 1]

 

Implementation of Minheap

class minheap:
    def __init__(self):
        self.A = []
    def min_heapify(self,k):
        l = 2 * k + 1
        r = 2 * k + 2
        smallest = k
        if l < len(self.A) and self.A[l] < self.A[smallest]:
            smallest = l
        if r < len(self.A) and self.A[r] < self.A[smallest]:
            smallest = r
        if smallest != k:
            self.A[k], self.A[smallest] = self.A[smallest], self.A[k]
            self.min_heapify(smallest)

    def build_min_heap(self,L):
        self.A = []
        for i in L:
            self.A.append(i)
        n = int((len(self.A)//2)-1)
        for k in range(n, -1, -1):
            self.min_heapify(k)

        
    def delete_min(self):
        item = None
        if self.A != []:
            self.A[0],self.A[-1] = self.A[-1],self.A[0]
            item = self.A.pop()
            self.min_heapify(0)
        return item


    def insert_in_minheap(self,d):
        self.A.append(d)
        index = len(self.A)-1
        while index > 0:
            parent = (index-1)//2
            if self.A[index] < self.A[parent]:
                self.A[index],self.A[parent] = self.A[parent],self.A[index]
                index = parent
            else:
                break

heap = minheap()
heap.build_min_heap([6,5,4,3,2])
print(heap.A)
heap.insert_in_minheap(1)
print(heap.A)
heap.insert_in_minheap(8)
print(heap.A)
print(heap.delete_min())
print(heap.delete_min())
print(heap.A)

Output

[2, 3, 4, 6, 5]
[1, 3, 2, 6, 5, 4]
[1, 3, 2, 6, 5, 4, 8]
1
2
[3, 5, 4, 6, 8]

Complexity

Heaps are a tree implementation of priority queues

• insert() is $O(log N)$
• delete max() is $O(log N)$
• heapify() builds a heap in $O(N)$

 

Improve Dijkstra's algorithm using min heap

Old implementation for adjacency matrix

def dijkstra(WMat,s):
    (rows,cols,x) = WMat.shape
    infinity = np.max(WMat)*rows+1
    (visited,distance) = ({},{})
    for v in range(rows):
        (visited[v],distance[v]) = (False,infinity)
        
    distance[s] = 0
    
    for u in range(rows):
        nextd = min([distance[v] for v in range(rows)
                        if not visited[v]])
        nextvlist = [v for v in range(rows)
                        if (not visited[v]) and
                            distance[v] == nextd]
        if nextvlist == []:
            break
        nextv = min(nextvlist)
        
        visited[nextv] = True        
        for v in range(cols):
            if WMat[nextv,v,0] == 1 and (not visited[v]):
                distance[v] = min(distance[v],distance[nextv]
                                                +WMat[nextv,v,1])
    return(distance)


dedges = [(0,1,10),(0,2,80),(1,2,6),(1,4,20),(2,3,70),(4,5,50),(4,6,5),(5,6,10)]
#edges = dedges + [(j,i,w) for (i,j,w) in dedges]
size = 7
import numpy as np
W = np.zeros(shape=(size,size,2))
for (i,j,w) in dedges:
    W[i,j,0] = 1
    W[i,j,1] = w
s = 0
print(dijkstra(W,s))

Output

{0: 0, 1: 10.0, 2: 16.0, 3: 86.0, 4: 30.0, 5: 80.0, 6: 35.0}

 

Updated Implementation for adjacency matrix using min heap

# considering dictionary as a heap for given code
def min_heapify(i,size):
        lchild = 2*i + 1
        rchild = 2*i + 2
        small = i
        if lchild < size-1 and HtoV[lchild][1] < HtoV[small][1]: 
        small = lchild
        if rchild < size-1 and HtoV[rchild][1] < HtoV[small][1]: 
        small = rchild
        if small != i:
            VtoH[HtoV[small][0]] = i
            VtoH[HtoV[i][0]] = small
            (HtoV[small],HtoV[i]) = (HtoV[i], HtoV[small])
            min_heapify(small,size)

def create_minheap(size):
        for x in range((size//2)-1,-1,-1):
        min_heapify(x,size)

def minheap_update(i,size):
    if i!= 0:
        while i > 0:
            parent = (i-1)//2
            if HtoV[parent][1] >  HtoV[i][1]:
                VtoH[HtoV[parent][0]] = i
                VtoH[HtoV[i][0]] = parent
                (HtoV[parent],HtoV[i]) = (HtoV[i], HtoV[parent])
            else:
                break
            i = parent

def delete_min(hsize):
        VtoH[HtoV[0][0]] = hsize-1
        VtoH[HtoV[hsize-1][0]] = 0
        HtoV[hsize-1],HtoV[0] = HtoV[0],HtoV[hsize-1]  
        node,dist = HtoV[hsize-1]
        hsize = hsize - 1
        min_heapify(0,hsize) 
        return node,dist,hsize

#global HtoV map heap index to (vertex,distance from source)
#global VtoH map vertex to heap index
HtoV, VtoH = {},{}
def dijkstra(WMat,s):
    (rows,cols,x) = WMat.shape
    infinity = float('inf')
    visited = {}
    heapsize = rows
    for v in range(rows):
        VtoH[v]=v
        HtoV[v]=[v,infinity]
        visited[v] = False
    HtoV[s]= [s,0]
    create_minheap(heapsize)
    
    for u in range(rows):
        nextd,ds,heapsize = delete_min(heapsize)             
        visited[nextd] = True        
        for v in range(cols):
            if WMat[nextd,v,0] == 1 and (not visited[v]):
                # update distance of adjacent of v if it is less than to previous one
                HtoV[VtoH[v]][1] = min(HtoV[VtoH[v]][1],ds+WMat[nextd,v,1])
                minheap_update(VtoH[v],heapsize)


dedges = [(0,1,10),(0,2,80),(1,2,6),(1,4,20),(2,3,70),(4,5,50),(4,6,5),(5,6,10)]
#edges = dedges + [(j,i,w) for (i,j,w) in dedges]
size = 7
import numpy as np
W = np.zeros(shape=(size,size,2))
for (i,j,w) in dedges:
    W[i,j,0] = 1
    W[i,j,1] = w
s = 0
dijkstra(W,s)
#print(HtoV)
#print(VtoH)
for i in range(size):
    print('Shortest distance from {0} to {1} = {2}'.format(s,i,HtoV[VtoH[i]][1]))

Output

Shortest distance from 0 to 0 = 0
Shortest distance from 0 to 1 = 10.0
Shortest distance from 0 to 2 = 16.0
Shortest distance from 0 to 3 = 86.0
Shortest distance from 0 to 4 = 30.0
Shortest distance from 0 to 5 = 80.0
Shortest distance from 0 to 6 = 35.0

 

Updated Implementation for adjacency list using min heap

def min_heapify(i,size):
    lchild = 2*i + 1
    rchild = 2*i + 2
    small = i
    if lchild < size-1 and HtoV[lchild][1] < HtoV[small][1]: 
        small = lchild
    if rchild < size-1 and HtoV[rchild][1] < HtoV[small][1]: 
        small = rchild
    if small != i:
        VtoH[HtoV[small][0]] = i
        VtoH[HtoV[i][0]] = small
        (HtoV[small],HtoV[i]) = (HtoV[i], HtoV[small])
        min_heapify(small,size)

def create_minheap(size):
    for x in range((size//2)-1,-1,-1):
        min_heapify(x,size)

def minheap_update(i,size):
    if i!= 0:
        while i > 0:
            parent = (i-1)//2
            if HtoV[parent][1] >  HtoV[i][1]:
                VtoH[HtoV[parent][0]] = i
                VtoH[HtoV[i][0]] = parent
                (HtoV[parent],HtoV[i]) = (HtoV[i], HtoV[parent])
            else:
                break
            i = parent

def delete_min(hsize):
    VtoH[HtoV[0][0]] = hsize-1
    VtoH[HtoV[hsize-1][0]] = 0
    HtoV[hsize-1],HtoV[0] = HtoV[0],HtoV[hsize-1]  
    node,dist = HtoV[hsize-1]
    hsize = hsize - 1
    min_heapify(0,hsize) 
    return node,dist,hsize


HtoV, VtoH = {},{}
#global HtoV map heap index to (vertex,distance from source)
#global VtoH map vertex to heap index
def dijkstralist(WList,s):
    infinity = float('inf')
    visited = {}
    heapsize = len(WList)
    for v in WList.keys():
        VtoH[v]=v
        HtoV[v]=[v,infinity]
        visited[v] = False
    HtoV[s]= [s,0]
    create_minheap(heapsize)
    
    for u in WList.keys():
        nextd,ds,heapsize = delete_min(heapsize)             
        visited[nextd] = True        
        for v,d in WList[nextd]:
            if not visited[v]:
                HtoV[VtoH[v]][1] = min(HtoV[VtoH[v]][1],ds+d)
                minheap_update(VtoH[v],heapsize)


dedges = [(0,1,10),(0,2,80),(1,2,6),(1,4,20),(2,3,70),(4,5,50),(4,6,5),(5,6,10)]
#edges = dedges + [(j,i,w) for (i,j,w) in dedges]
size = 7
WL = {}
for i in range(size):
    WL[i] = []
for (i,j,d) in dedges:
    WL[i].append((j,d))
s = 0
dijkstralist(WL,s)
#print(HtoV)
#print(VtoH)
for i in range(size):
    print('Shortest distance from {0} to {1} = {2}'.format(s,i,HtoV[VtoH[i]][1]))

Output

Shortest distance from 0 to 0 = 0
Shortest distance from 0 to 1 = 10
Shortest distance from 0 to 2 = 16
Shortest distance from 0 to 3 = 86
Shortest distance from 0 to 4 = 30
Shortest distance from 0 to 5 = 80
Shortest distance from 0 to 6 = 35

Complexity

Using min-heaps:-

• Identifying next vertex to visit is $O(log n)$
• Updating distance takes $O(log n)$ per neighbor
• Adjacency list — proportionally to degree

Cumulatively:-

• $O(n log n)$ to identify vertices to visit across n iterations
• $O(m log n)$ distance updates overall
• Overall $O((m + n) log n)$

 

Heap Sort

Implementation

def max_heapify(A,size,k):
    l = 2 * k + 1
    r = 2 * k + 2
    largest = k
    if l < size and A[l] > A[largest]:
        largest = l
    if r < size and A[r] > A[largest]:
        largest = r
    if largest != k:
        (A[k], A[largest]) = (A[largest], A[k])
        max_heapify(A,size,largest)

def build_max_heap(A):
    n = (len(A)//2)-1
    for i in range(n, -1, -1):
        max_heapify(A,len(A),i)

def heapsort(A):
    build_max_heap(A)
    n = len(A)
    for i in range(n-1,-1,-1):
        A[0],A[i] = A[i],A[0]
        max_heapify(A,i,0)
        

A = [8,6,9,3,4,5,61,6666]
heapsort(A)
print(A)

Output

[3, 4, 5, 6, 8, 9, 61, 6666]

Complexity

• Start with an unordered list
• Build a heap — $O(n)$
• Call delete max() n times to extract elements in descending order — $O(n log n)$
• After each delete max(), heap shrinks by 1
• Store maximum value at the end of current heap
• In place $O(n log n)$ sort

 

Binary Search Tree(BST)

For dynamic stored data

• Sorting is useful for efficient searching
• What if the data is changing dynamically?
• Items are periodically inserted and deleted Insert/delete in a sorted list takes time O(n)

How can we improve Insert/delete time? - using tree structure?

A binary search tree is a binary tree that is either empty or satisfies the following conditions:

For each node V in the Tree

• The value of the left child or left subtree is always less than the value of V.
• The value of the right child or right subtree is always greater than the value of V.

Visualization

Open Visualization

https://visualgo.net/en/bst

Implementation

class Tree:
# Constructor:
    def __init__(self,initval=None):
        self.value = initval
        if self.value:
            self.left = Tree()
            self.right = Tree()
        else:
            self.left = None
            self.right = None
        return
    # Only empty node has value None
    def isempty(self):
        return (self.value == None)
    # Leaf nodes have both children empty
    def isleaf(self):
        return (self.value != None and self.left.isempty() and self.right.isempty())
    # Inorder traversal
    def inorder(self):
        if self.isempty():
            return([])
        else:
            return(self.left.inorder()+[self.value]+self.right.inorder())
        # Display Tree as a string
    def __str__(self):
        return(str(self.inorder()))
    # Check if value v occurs in tree
    def find(self,v):
        if self.isempty():
            return(False)
        if self.value == v:
            return(True)
        if v < self.value:
            return(self.left.find(v))
        if v > self.value:
            return(self.right.find(v))
    # return minimum value for tree rooted on self - Minimum is left most node in the tree
    def minval(self):
        if self.left.isempty():
            return(self.value)
        else:
            return(self.left.minval())
    # return max value for tree rooted on self  - Maximum is right most node in the tree
    def maxval(self):
        if self.right.isempty():
            return(self.value)
        else:
            return(self.right.maxval())
    # insert new element in binary search tree
    def insert(self,v):
        if self.isempty():
            self.value = v
            self.left = Tree()
            self.right = Tree()
        if self.value == v:
            return
        if v < self.value:
            self.left.insert(v)
            return
        if v > self.value:
            self.right.insert(v)
            return
    # delete element from binary search tree
    def delete(self,v):
        if self.isempty():
            return
        if v < self.value:
            self.left.delete(v)
            return
        if v > self.value:
            self.right.delete(v)
            return
        if v == self.value:
            if self.isleaf():
                self.makeempty()
            elif self.left.isempty():
                self.copyright()
            elif self.right.isempty():
                self.copyleft()
            else:
                self.value = self.left.maxval()
                self.left.delete(self.left.maxval())
            return
    # Convert leaf node to empty node
    def makeempty(self):
        self.value = None
        self.left = None
        self.right = None
        return
    # Promote left child
    def copyleft(self):
        self.value = self.left.value
        self.right = self.left.right
        self.left = self.left.left
        return
    # Promote right child
    def copyright(self):
        self.value = self.right.value
        self.left = self.right.left
        self.right = self.right.right
        return

    

T = Tree()
bst = [9,8,7,6,5,4,3,2,1]
k = 4
for i in bst:
    T.insert(i)
print('Element in BST are:= ',T.inorder())
print('Maximum element in BST are:= ',T.maxval())
print('Minimum element in BST are:= ',T.minval())
print(k,'is present or not = ',T.find(k))
T.delete(3)
print('Element in BST after delete 3:= ',T.inorder())

Output

Element in BST are:=  [1, 2, 3, 4, 5, 6, 7, 8, 9]
Maximum element in BST are:=  9
Minimum element in BST are:=  1
4 is present or not =  True
Element in BST after delete 3:=  [1, 2, 4, 5, 6, 7, 8, 9]

Complexity

• find(), insert() and delete() all walk down a single path
• Worst-case: height of the tree
• An unbalanced tree with n nodes may have height $O(n)$
• Balanced trees have height $O(log n)$
• Will see how to keep a tree balanced to ensure all operations remain $O(log n)$