Divide and conquer

• Break up a problem into disjoint subproblems

• Combine these subproblem solutions efficiently

• Examples

  • Merge sort

    • Split into left and right half and sort each half separately
    • Merge the sorted halves

  • Quicksort

    • Rearrange into lower and upper partitions, sort each partition separately
    • Place pivot between sorted lower and upper partitions

 

Divide and conquer example

Counting inversions

• Compare your profile with other customers

• Identify people who share your likes and dislikes

• No inversions – rankings identical

• Every pair inverted – maximally dissimilar

• Number of inversions ranges from 0 to n(n – 1) / 2

  

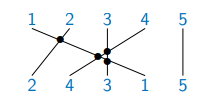
• An inversion is a pair (i, j), i < j, where j appears before i

• Recurrence: $T(n) = 2T(n / 2) + n = 𝑂(n log 𝑛)$

 

Implementation

def mergeAndCount(A,B):
    (m,n) = (len(A),len(B))
    (C,i,j,k,count) = ([],0,0,0,0)
    while k < m+n:
        if i == m:
            C.append(B[j])
            j += 1
            k += 1
        elif j == n:
            C.append(A[i])
            i += 1
            k += 1
        elif A[i] < B[j]:
            C.append(A[i])
            i += 1
            k += 1
        else:
            C.append(B[j])
            j += 1
            k += 1
            count += m-i            
    return(C,count)

def inversionCount(A):
    n = len(A)
    if n <= 1:
        return(A,0)
    (L,countL) = inversionCount(A[:n//2])
    (R,countR) = inversionCount(A[n//2:])
    (B,countB) = mergeAndCount(L,R)
    return(B,countL + countR + countB)
L = [2,4,3,1,5]
print(inversionCount(L)[1])

Output

4 # 4 is the number of inversions

 

Closest pair of points

• Several objects on screen

• Basic step: find closest pair of objects

• $n$ objects — naive algorithm is $n^2$

  • For each pair of objects, compute their distance
  • Report minimum distance across all pairs

• There is a clever algorithm that takes time $O(n log n)$ using divide and conquer

• Given n points $p1, p2, . . . , pn$ find the closest pair

  • Assume no two points have same $x$ or $y$ coordinate
  • Split the points into two halves by vertical line
  • Recursively compute closest pair in each half
  • Compare shortest distance in each half to shortest distance across the dividing line

• Recurrence: $𝑇 𝑛 = 2𝑇 𝑛 / 2 + 𝑂(𝑛)$

• Overall: $𝑂(𝑛 log 𝑛)$

Pseudocode

def ClosestPair(Px,Py):
    if len(Px) <= 3:
        compute pairwise distances
        return closest pair and distance
    Construct (Qx,Qy), (Rx,Ry)
    (q1,q2,dQ) = ClosestPair(Qx,Qy)
    (r1,r2,dR) = ClosestPair(Rx,Ry)
    Construct Sy from Qy,Ry
    Scan Sy, find (s1,s2,dS)
    return (q1,q2,dQ), (r1,r2,QR), (s1,s2,dS)
    #depending on which of dQ, dR, dS is minimum

Implementation

import math

# Returns eucledian disatnce between points p and q
def distance(p, q):
  return math.sqrt(math.pow(p[0] - q[0],2) + math.pow(p[1] - q[1],2))

def minDistanceRec(Px, Py):
  s = len(Px)
  # Given number of points cannot be less than 2.
  # If only 2 or 3 points are left return the minimum distance accordingly.
  if (s == 2):
    return distance(Px[0],Px[1])
  elif (s == 3):
    return min(distance(Px[0],Px[1]), distance(Px[1],Px[2]), distance(Px[2],Px[0]))

  # For more than 3 points divide the poitns by point around median of x coordinates
  m = s//2
  Qx = Px[:m]
  Rx = Px[m:]
  xR = Rx[0][0]    # minimum x value in Rx
  
  # Construct Qy and Ry in O(n) rather from Py
  Qy=[]
  Ry=[]
  for p in Py:
    if(p[0] < xR):
      Qy.append(p)
    else:
      Ry.append(p)

  # Extract Sy using delta
  delta = min(minDistanceRec(Qx, Qy), minDistanceRec(Rx, Ry))
  Sy = []
  for p in Py:
    if abs(p[0]-xR) <= delta:
      Sy.append(p)
    
  #print(xR,delta,Sy)
  sizeS = len(Sy)
  if sizeS > 1:
      minS = distance(Sy[0], Sy[1])
      for i in range(1, sizeS-1):
          for j in range(i, min(i+15, sizeS-1)):
              minS = min(minS, distance(Sy[i], Sy[j+1]))
      return min(delta, minS)
  else:
      return delta

def minDistance(Points):
  Px = sorted(Points)
  Py = Points
  Py.sort(key=lambda x: x[-1])
  #print(Px,Py)
  return round(minDistanceRec(Px, Py), 2)



pts =  [(2, 15), (40, 5), (20, 1), (21, 14), (1,4), (3, 11)]
result = minDistance(pts)
print(result)

Output

4.12

 

Integer multiplication

• Traditional method: $𝑂(𝑛 ^2 )$
• Naïve divide and conquer strategy: $𝑇(𝑛) = 4𝑇(𝑛 / 2) + 𝑛 = 𝑂(𝑛^2 )$
• Karatsuba’s algorithm: $𝑇(𝑛) = 3𝑇 𝑛 / 2 + 𝑛 ≈ 𝑂 𝑛 ~log~3)$

Implementation

# here 10 represent base of input numbers x and y
def Fast_Multiply(x,y,n):
    if n == 1:
        return x * y
    else:
        m = n/2
        xh = x//10**m
        xl = x % (10**m)
        yh = y//10**m
        yl = y % (10**m)
        a = xh + xl
        b = yh + yl
        p = Fast_Multiply(xh, yh, m)
        q = Fast_Multiply(xl, yl, m)
        r = Fast_Multiply(a, b, m)
        return p*(10**n) + (r - q - p) * (10**(n/2)) + q 
print(Fast_Multiply(3456,8902,4))

Output

30765312.0

 

Quick select and Fast select

• Find the $𝑘_{𝑡ℎ}$ smallest value in a sequence of length $𝑘$
• Sort in descending order and look at position $𝑘~ –~ 𝑂 (𝑛 log 𝑛)$
• For any fixed $𝑘$, find maximum for $𝑘$ times – $𝑂(𝑘𝑛)$
• $𝑘 = n / 2$ (median) – $𝑂 (𝑛^2)$
• Median of medians –$𝑂(𝑛)$
• Selection becomes $𝑂(𝑛)$ in Fast select algorithm
• Quicksort becomes $𝑂 (𝑛 log n)$ using MoM

Implementation

def quickselect(L,l,r,k): # k-th smallest in L[l:r]
  if (k < 1) or (k > r-l):
    return(None)

  (pivot,lower,upper) = (L[l],l+1,l+1)
  for i in range(l+1,r):
    if L[i] > pivot:  # Extend upper segment
      upper = upper + 1
    else: # Exchange L[i] with start of upper segment
      (L[i], L[lower]) = (L[lower], L[i])
      (lower,upper) = (lower+1,upper+1)
  (L[l],L[lower-1]) = (L[lower-1],L[l]) # Move pivot
  lower = lower - 1

  # Recursive calls
  lowerlen = lower - l
  if k <= lowerlen:
    return(quickselect(L,l,lower,k))
  elif k == (lowerlen + 1):
    return(L[lower])
  else:
    return(quickselect(L,lower+1,r,k-(lowerlen+1)))
print(quickselect([5,3,7,2,1],0,5,2))

Output

2

 

Median of Medians(MoM)

• Divide L into blocks of 5

• Find the median of each block (brute force)

• Let M be the list of block medians

• Recursively apply the process to M

• We can visualize the blocks as follows

  

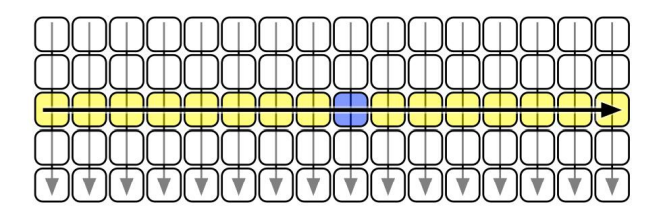
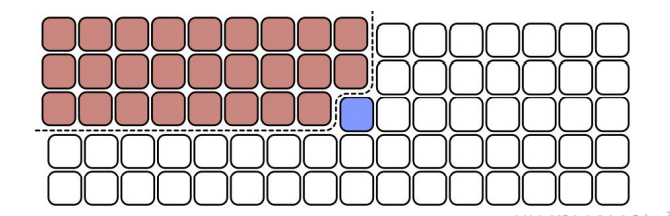
• Each block of 5 is arranged in ascending order, top to bottom

• Block medians are the middle row

• The median of block medians lies between 3len(L)/10 and 7len(L)/10

  

Implementation

def MoM(L): # Median of medians
  if len(L) <= 5:
    L.sort()
    return(L[len(L)//2])
  # Construct list of block medians
  M = []
  for i in range(0,len(L),5):
    X = L[i:i+5]
    X.sort()
    M.append(X[len(X)//2])
  return(MoM(M))
print(MoM([4,3,5,6,2,1,8,9,7,10,13,15,18,17,11]))

Output

8

 

Fast select using MOM

Implementation

def MoM(L): # Median of medians
  if len(L) <= 5:
    L.sort()
    return(L[len(L)//2])
  # Construct list of block medians
  M = []
  for i in range(0,len(L),5):
    X = L[i:i+5]
    X.sort()
    M.append(X[len(X)//2])
  return(MoM(M))



def fastselect(L,l,r,k): # k-th smallest in L[l:r]
  if (k < 1) or (k > r-l):
    return(None)

  # Find MoM pivot and move to L[l]
  pivot = MoM(L[l:r])
  pivotpos = min([i for i in range(l,r) if L[i] == pivot])
  (L[l],L[pivotpos]) = (L[pivotpos],L[l])

  (pivot,lower,upper) = (L[l],l+1,l+1)
  for i in range(l+1,r):
    if L[i] > pivot:  # Extend upper segment
      upper = upper + 1
    else: # Exchange L[i] with start of upper segment
      (L[i], L[lower]) = (L[lower], L[i])
      (lower,upper) = (lower+1,upper+1)
  (L[l],L[lower-1]) = (L[lower-1],L[l]) # Move pivot
  lower = lower - 1
  
  # Recursive calls
  lowerlen = lower - l
  if k <= lowerlen:
    return(fastselect(L,l,lower,k))
  elif k == (lowerlen + 1):
    return(L[lower])
  else:
    return(fastselect(L,lower+1,r,k-(lowerlen+1)))
print(fastselect([4,3,5,6,2,1,8,9,7,10,13,15,18,17,11],0,15,4))

Output

4

 

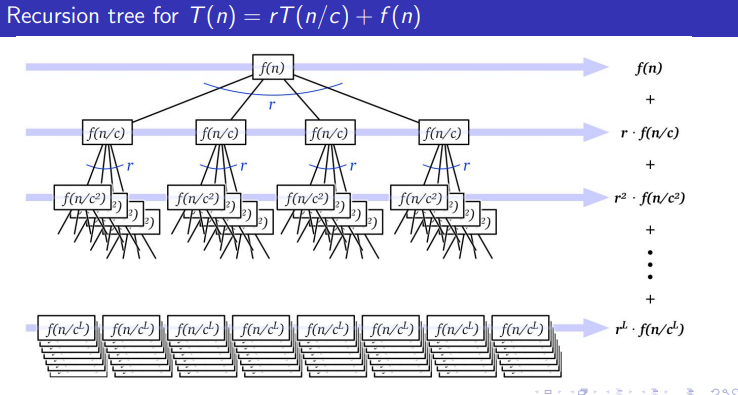
Recursion trees

• Recursion tree-Rooted tree with one node for each recursive subproblem

• Value of each node is time spent on that subproblem excluding recursive calls

• Concretely, on an input of size $n$

  • $f (n)$ is the time spent on non-recursive work
  • $r$ is the number of recursive calls
  • Each recursive call works on a subproblem of size $n/c$

• Resulting recurrence: $T(n) = rT(n/c) + f (n)$

• Root of recursion tree for $T(n)$ has value $f (n)$

• Root has $r$ children, each (recursively) the root of a tree for $T(n/c)$

• Each node at level $d$ has value $f (n/c^d )$

  • Assume, for simplicity, that $n$ was a power of $c$