Dynamic programming
Solution to original problem can be derived by combining solutions to subproblems
Examples: Factorial, Insertion sort, Fibonacci series
Anticipate the structure of subproblems
Derive from inductive definition
Solve subproblems in topological order
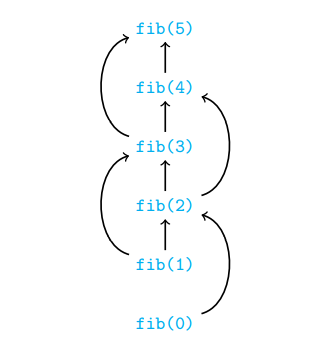
Memoization
- Inductive solution generates same subproblem at different stages
- Naïve recursive implementation evaluates each instance of subproblem from scratch
- Build a table of values already computed – Memory table
- Store each newly computed value in a table
- Look up the table before making a recursive call
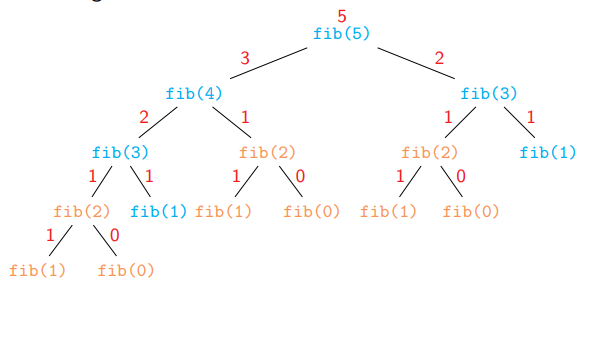
Example of
Simple recursive
def fibrec(n):
if n <= 1:
return n
return fibrec(n - 1) + fibrec(n - 2)
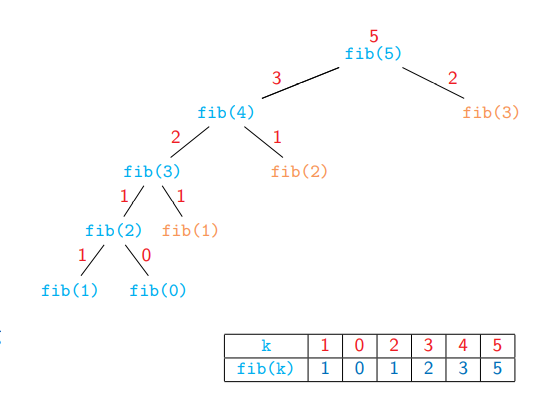
Memoization
memo ={}
def fib(n):
if n <= 1:
memo[n] = n
if n not in memo:
memo[n] = fib(n-1) + fib(n-2)
return memo[n]
Dynamic programming
def fib(n):
T = [0] * (n + 1)
T[1] = 1
for i in range(2, n + 1):
T[i] = T[i - 1] + T[i - 2]
return T[n]
Comparison
#simple recursive
def fibrec(n):
if n <= 1:
return n
return fibrec(n - 1) + fibrec(n - 2)
# memoization topdown
memo ={}
def fibmem(n):
if n <= 1:
memo[n] = n
if n not in memo:
memo[n] = fibmem(n-1) + fibmem(n-2)
return memo[n]
# DP tabulation bottom up
def fibtab(n):
T = [0] * (n + 1)
T[1] = 1
for i in range(2, n + 1):
T[i] = T[i - 1] + T[i - 2]
return T[n]
n=int(input())
import time
t1 = time.perf_counter()
res1 = fibrec(n)
ft1 = time.perf_counter() - t1
t1 = time.perf_counter()
res2 = fibmem(n)
ft2 = time.perf_counter() - t1
t1 = time.perf_counter()
res3 = fibtab(n)
ft3 = time.perf_counter() - t1
print(res1,ft1)
print(res2,ft2)
print(res3,ft3)
Dynamic programming problems
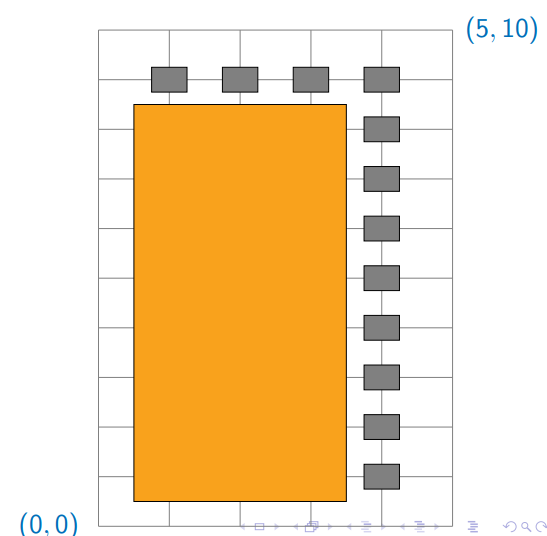
Grid path Problem
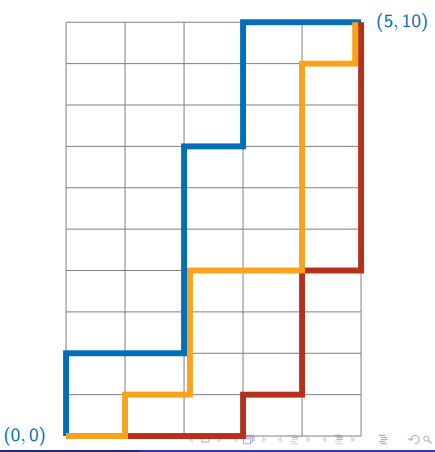
Rectangular grid of one-way roads
Can only go up and right
How many paths from (0, 0) to
? Every path has
segments What if an intersection is blocked?
Need to discard paths passing through blocked intersection
Inductive structure

Fill the grid by row, column or diagonal

Memoization vs dynamic programming
Barrier of holes just inside the border
Memoization never explores the shaded region
Memo table has O(m + n) entries
Dynamic programming blindly fills all mn cells of the table
Tradeoff between recursion and iteration
- “Wasteful” dynamic programming still better in general
- Complexity is
using dynamic programming, using memorization
Implementation for Grid Path problem:
Simple recursive
def grid_rec(x,y,barrier):
global count
count+=1
if x < 1 or y < 1:
return 1
elif (x,y) in barrier:
return 0
else:
return grid_rec(x-1,y,barrier) + grid_rec(x,y-1,barrier)
count = 0
barrier = [(1,9),(2,9),(3,9),(4,9),(4,8),(4,7),(4,6),(4,5),(4,4),(4,3),(4,2),(4,1)]
print("Total path= ",grid_rec(5,10,barrier))
print("recursive call count= ",count)
Memoization
def grid_memo(x,y):
global count
count+=1
if (x,y) in memo_table:
return memo_table[(x,y)]
else:
memo_table[(x,y)] = grid_memo(x-1,y) + grid_memo(x,y-1)
return memo_table[(x,y)]
count = 0
memo_table = {}
for i in range(6):
memo_table[(i,0)]=1
for i in range(11):
memo_table[(0,i)]=1
barrier = [(1,9),(2,9),(3,9),(4,9),(4,8),(4,7),(4,6),(4,5),(4,4),(4,3),(4,2),(4,1)]
for k in barrier:
if (k[0],k[1]) not in memo_table.keys():
memo_table[(k[0],k[1])] = 0
print("Total path= ",grid_memo(5,10))
print("recursive call count= ",count)
Dynamic programming
import numpy as np
def grid_tab(x,y,barrier):
M = np.zeros((x+1,y+1))
for i in range(x+1):
for j in range(y+1):
if i == 0 or j == 0:
M[i,j] = 1
for i in range(1,x+1):
for j in range(1,y+1):
if (i,j) in barrier:
M[i,j] = 0
else:
M[i,j] = M[i-1,j] + M[i,j-1]
print (M)
return int(M[x,y])
barrier = [(1,9),(2,9),(3,9),(4,9),(4,8),(4,7),(4,6),(4,5),(4,4),(4,3),(4,2),(4,1)]
print("Total path= ",grid_tab(5,10,barrier))
Longest Common Sub Word (LCW)
- Given two strings, find the (length of the) longest common sub word
- Subproblems are LCW(i, j), for 0 ≤ 𝑖 ≤ 𝑚, 0 ≤ 𝑗 ≤ 𝑛
- Table of 𝑚 + 1 𝑛 + 1 values
- Inductive structure
Start at bottom right and fill row by row or column by column
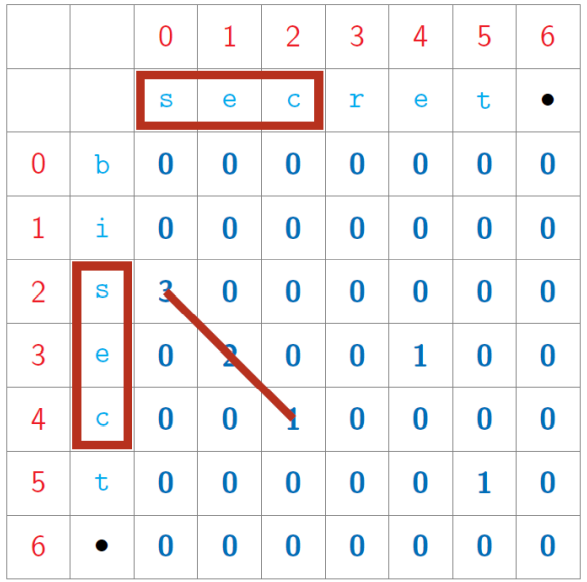
Implementation
def LCW(s1,s2):
import numpy as np
(m,n) = (len(s1),len(s2))
lcw = np.zeros((m+1,n+1))
maxw = 0
for c in range(n-1,-1,-1):
for r in range(m-1,-1,-1):
if s1[r] == s2[c]:
lcw[r,c] = 1 + lcw[r+1,c+1]
else:
lcw[r,c] = 0
if lcw[r,c] > maxw:
maxw = lcw[r,c]
return maxw
s1 = 'bisect'
s2 = 'secret'
print(LCW(s1,s2))
Output
3.0
Complexity
Longest Common Subsequence (LCS)
- Subsequence – can drop some letters in between
- Subproblems are LCS(i, j), for 0 ≤ 𝑖 ≤ 𝑚, 0 ≤ 𝑗 ≤ 𝑛
- Table of 𝑚 + 1 𝑛 + 1 values
- Inductive structure
- Start at bottom right and fill row by row, column or diagonal
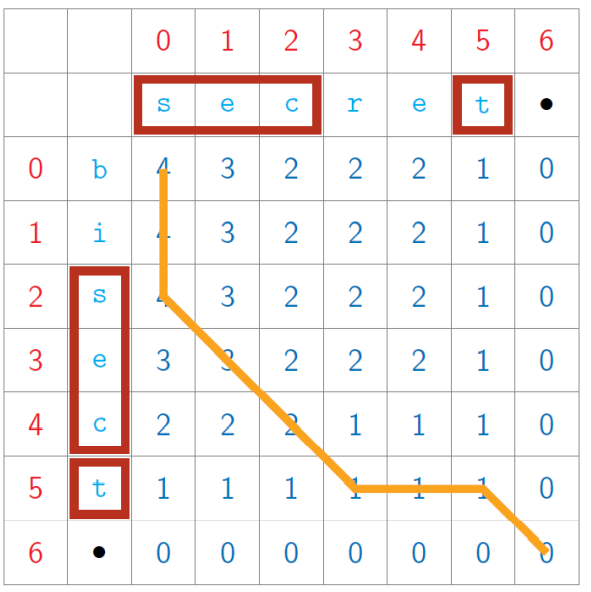
Implementation
def LCS(s1,s2):
import numpy as np
(m,n) = (len(s1),len(s2))
lcs = np.zeros((m+1,n+1))
for c in range(n-1,-1,-1):
for r in range(m-1,-1,-1):
if s1[r] == s2[c]:
lcs[r,c] = 1 + lcs[r+1,c+1]
else:
lcs[r,c] = max(lcs[r+1,c], lcs[r,c+1])
return lcs[0,0]
s1 = 'secret'
s2 = 'bisect'
print(LCS(s1,s2))
Output
4.0
Complexity
Edit distance
- Minimum number of editing operations needed to transform one document to the other
- Subproblems are ED(i, j), for 0 ≤ 𝑖 ≤ 𝑚, 0 ≤ 𝑗 ≤ 𝑛
- Table of 𝑚 + 1 𝑛 + 1 values ▪
- Inductive structure
Start at bottom right and fill row, column or diagonal
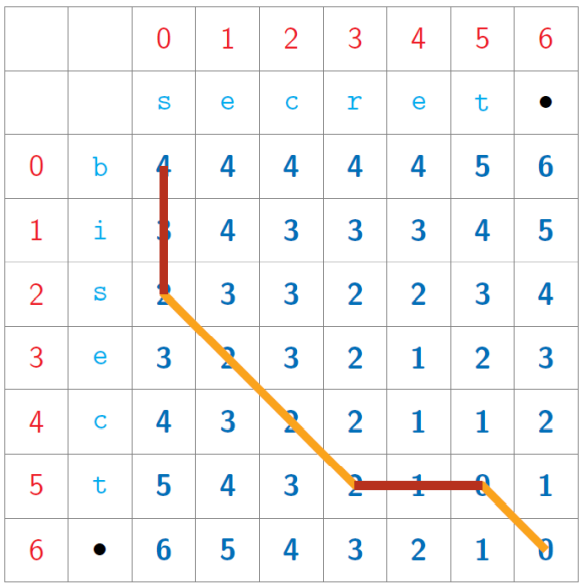
Implementation
def ED(u,v):
import numpy as np
(m,n) = (len(u),len(v))
ed = np.zeros((m+1,n+1))
for i in range(m-1,-1,-1):
ed[i,n] = m-i
for j in range(n-1,-1,-1):
ed[m,j] = n-j
for j in range(n-1,-1,-1):
for i in range(m-1,-1,-1):
if u[i] == v[j]:
ed[i,j] = ed[i+1,j+1]
else:
ed[i,j] = 1 + min(ed[i+1,j+1], ed[i,j+1], ed[i+1,j])
return(ed[0,0])
print(ED('bisect','secret'))
Output
4.0
Complexity
Matrix multiplication
Matrix multiplication is associative
Bracketing does not change answer but can affect the complexity
Find an optimal order to compute the product
Compute C ( i, j), 0 ≤ 𝑖, 𝑗 < 𝑛, only for 𝑖 ≤ 𝑗
C ( i, j), depends on C ( i, k – 1) , C( k, j) for every 𝑖 < 𝑘 ≤ 𝑗
Diagonal entries are base case, fill matrix from main diagonal
Implementation
def MM(dim):
n = dim.shape[0]
C = np.zeros((n,n))
for i in range(n):
C[i,i] = 0
for diff in range(1,n):
for i in range(0,n-diff):
j = i + diff
C[i,j] = C[i,i] + C[i+1,j] + dim[i][0] * dim[i+1][0] * dim[j][1]
print(C)
for k in range(i+1, j+1):
C[i,j] = min(C[i,j],C[i,k-1] + C[k,j] + dim[i][0] * dim[k][0] * dim[j][1])
print(C)
return(C[0,n-1])
import numpy as np
a = np.array([[2,3],[3,4],[4,5]])
print(MM(a))
Output
64
Complexity
Other implementation
Inductive structure
def MM(dim):
n = len(dim)
C = []
for i in range(n):
L = []
L=[0]*n
C.append(L.copy())
for diff in range(1,n):
for i in range(0,n-diff):
j = i + diff
KL = []
for k in range(i, j):
KL.append(C[i][k] + C[k+1][j] + dim[i][0] * dim[k][1] * dim[j][1])
C[i][j] = min(KL)
return(C[0][n-1])
a = [[4,10],[10,3],[3,12],[12,20],[20,7]]
print(MM(a))
Output
1344
Complexity
Example
For example, we have matrices {M0, M1, M2, M3, M4} and the dimensions list of the given matrices is [[4,10],[10,3],[3,12],[12,20],[20,7]].
Matrix C : -
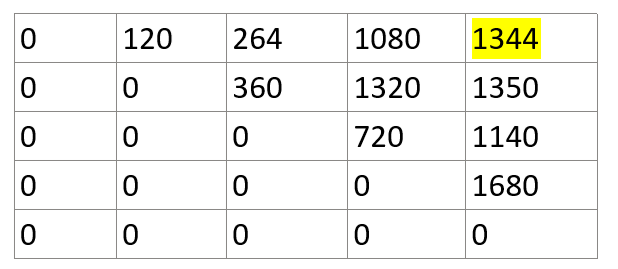
Here 1344 value is representing minimum number of multiplication steps.
We can identify the order of multiplication of matrix by storing the k value(value of k for which we get minimum steps) in matrix with steps.
Matrix C : -
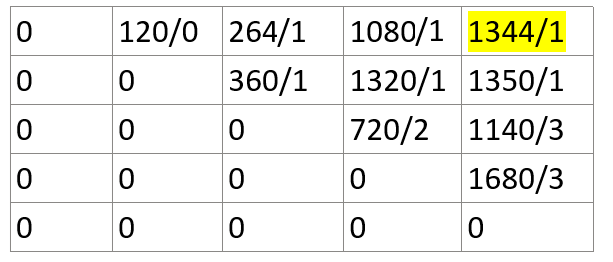
So initially we have matrices {M0, M1, M2, M3, M4} and at a time 2 matrices we can multiply.
We will check the k value for C[0][4] which is 1, so we can parenthesize the order like{(M0 M1)(M2 M3 M4)} now we have to check the order in the second bracket matrix M2, M3, M4, so we will check the value C[2][4] which is 3 then we can parenthesize the order like ((M2 M3) M4) So, the final order will be (M0 M1)((M2 M3) M4).