---

Home Week-9

---

 

PDSA - Week 12 (As Extra Content)

String matching

Searching for a pattern is a fundamental problem when dealing with text

• Editing a document

• Answering an internet search query

• Looking for a match in a gene sequence

Example

• an occurs in banana at two positions

Formally

• A text string t of length n A pattern string p of length m

• Both t and p are drawn from an alphabet of valid letters, denoted Σ

• Find every position i in t such that t[i:i+m] == p

Brute force approach

Nested scan from left to right in t

1
def stringmatch(t,p):
2
    poslist = []
3
    for i in range(len(t)-len(p)+1):
4
        matched = True
5
        j = 0
6
        while j < len(p) and matched:
7
            if t[i+j] != p[j]:
8
                matched = False
9
            j = j+1
10
        if matched:
11
            poslist.append(i)
12
    return(poslist)
13
print(stringmatch('abababbababbbbababab','abab'))

Output

xxxxxxxxxx
1
1
[0, 2, 7, 14, 16]

Complexity

$O(nm)$$O(nm)$

 

Nested scan from right to left

xxxxxxxxxx
13
1
def stringmatchrev(t,p):
2
    poslist = []
3
    for i in range(len(t)-len(p)+1):
4
        matched = True
5
        j = len(p)-1
6
        while j >= 0 and matched:
7
            if t[i+j] != p[j]:
8
                matched = False
9
            j = j-1
10
        if matched:
11
            poslist.append(i)
12
    return(poslist)
13
print(stringmatchrev('abababbababbbbababab','abab'))

Output

xxxxxxxxxx
1
1
[0, 2, 7, 14, 16]

Complexity

$O(nm)$$O(nm)$

 

Speeding up the brute force algorithm

• Text t, pattern p of of lengths n, m

• For each starting position i in t, compare t[i:i+m] with p

  • Scan t[i:i+m] right to left

• While matching, we find a letter in t that does not appear in p

  • t = bananamania, p = bulk

• Shift the next scan to position after mismatched letter

• What if the mismatched letter does appear in p?

 

Boyer-Moore Algorithm

Algorithm

• Initialize last[c] for each c in p

  • Single scan, rightmost value is recorded

• Nested loop, compare each segment t[i:i+len(p)] with p

• If p matches, record and shift by 1

• We find a mismatch at t[i+j]

  • If j > last[t[i+j]], shift by j - last[t[i+j]]

  • If last[t[i+j]] > j, shift by 1

    • Should not shift p to left!

  • If t[i+j] not in p, shift by j+1

Implementation

xxxxxxxxxx
23
1
def boyermoore(t,p):
2
    last = {} # Preprocess
3
    for i in range(len(p)):
4
        last[p[i]] = i
5
    poslist=[]
6
    i = 0
7
    while i <= (len(t)-len(p)):
8
        matched,j = True,len(p)-1
9
        while j >= 0 and matched:
10
            if t[i+j] != p[j]:
11
                matched = False
12
            j = j - 1
13
        if matched:
14
            poslist.append(i)
15
            i = i + 1
16
        else:
17
            j = j + 1
18
            if t[i+j] in last.keys():
19
                i = i + max(j-last[t[i+j]],1)
20
            else:
21
                i = i + j + 1
22
    return(poslist)
23
print(boyermoore('abcaaacabc','abc'))

Output

xxxxxxxxxx
1
1
[0, 7]

Complexity

Worst case remains $O(nm)$$O(nm)$

If t = aaa...a, p = baaa

 

Rabin-Karp Algorithm

• Suppose Σ = {0, 1, . . . , 9}

• Any string over Σ can be thought of as a number in base 10

• Pattern $p$$p$ is an $m$$m$-digit number $n_p$$n_p$

• Each substring of length $m$$m$ in the text $t$$t$ is again an $m$$m$-digit number

• Scan $t$$t$ and compare the number $n_b$$n_b$ generated by each block of $m$$m$ letters with the pattern number $n_p$$n_p$

Implementation

xxxxxxxxxx
15
1
def rabinkarp(t,p):
2
    poslist = []
3
    numt,nump = 0,0
4
    for i in range(len(p)):
5
        numt = 10*numt + int(t[i])
6
        nump = 10*nump + int(p[i])
7
    if numt == nump:
8
        poslist.append(0)
9
    for i in range(1,len(t)-len(p)+1):
10
        numt = numt - int(t[i-1])*(10**(len(p)-1))
11
        numt = 10*numt + int(t[i+len(p)-1])
12
        if numt == nump:
13
            poslist.append(i)
14
    return(poslist)
15
print(rabinkarp('233323233454323','23'))

Output

xxxxxxxxxx
1
1
[0, 4, 6, 13]

Analysis

• Preprocessing time is $O(m)$$O(m)$

  • To convert t[0:m], p to numbers

• Worst case for general alphabets is $O(nm)$$O(nm)$

  • Every block t[i:i+m] may have same remainder modulo q as the pattern p

  • Must validate each block explicitly, like brute force

• In practice number of spurious matches will be small

• If |Σ| is small enough to not require modulo arithmetic, overall time is $O(n+m)$$O(n + m)$, or $O(n)$$O(n)$, since $m<<n$$m << n$

  • Also if we can choose q carefully to ensure $O(1)$$O(1)$ spurious matches

 

Rabin Karp Implementation for strings

xxxxxxxxxx
31
1
def rabin_karp(text, pattern):
2
    match_found =[]
3
    n = len(text)
4
    m = len(pattern)    
5
    # Prime number to use for the hash function
6
    prime = 101   
7
    # Calculate the hash value of the pattern
8
    pattern_hash = 0
9
    for i in range(m):
10
        pattern_hash += ord(pattern[i])
11
    pattern_hash = pattern_hash % prime
12
    
13
    # Calculate the hash value of the first substring of the text
14
    text_hash = 0
15
    for i in range(m):
16
        text_hash += ord(text[i])
17
    text_hash = text_hash % prime
18
    # Iterate through the text, checking for matches with the pattern
19
    for i in range(n - m + 1):
20
        # Check if the current substring matches the pattern
21
        if text_hash == pattern_hash and text[i:i+m] == pattern:
22
            match_found.append(i)       
23
        # Calculate the hash value of the next substring
24
        if i < n - m:
25
            text_hash = (text_hash - ord(text[i]) + ord(text[i+m]))
26
            text_hash = text_hash % prime
27
    # No match found
28
    return match_found
29
text = 'abcdbabcdb'
30
pattern = 'abcdb'
31
print(rabin_karp(text, pattern))

Output

xxxxxxxxxx
1
1
[0, 5]

 

 

Knuth-Morris-Pratt algorithm

• Compute the automaton for p efficiently

• Match p against itself

  • match[j] = kif suffix of p[:j+1] matches prefix p[:k]

• Suppose suffix of p[:j+1] matches prefix p[:k]

  • If p[j+1] == p[k], extend the match

  • Otherwise try to find a shorter prefix that can be extended by p[j+1]

• Usually refer to match as failure function fail

  • Where to fall back if match fails

Computing the fail function

• Initialize fail[j] = 0 for all j

• k keeps track of length of current match

• j is next position to update fail

• If p[j] == p[k] extend the match, set fail[j] = k+1

• If p[j] != p[k] find a shorter prefix that matches suffix of p[:j]

  • Step back to fail[k-1]

• If we don’t find a nontrivial prefix to extend, retain fail[j] = 0, move to next position

Implementation of fail function

xxxxxxxxxx
14
1
def kmp_fail(p):
2
    m = len(p)
3
    fail = [0 for i in range(m)]
4
    j,k = 1,0
5
    while j < m:
6
        if p[j] == p[k]:
7
            fail[j] = k+1
8
            j,k = j+1,k+1
9
        elif k > 0:
10
            k = fail[k-1]
11
        else:
12
            j = j+1
13
    return(fail)
14
print(kmp_fail('abcaabca'))

Output

xxxxxxxxxx
1
1
[0, 0, 0, 1, 1, 2, 3, 4]

Complexity

$O(n)$$O(n)$

 

Implementation of KMP algorithm

• Scan t from beginning

• j is next position in t

• k is currently matched position in p

• If t[j] == p[k] extend the match

• If t[j] != p[k], update match prefix

• If we reach the end of the while loop, no match

​x
1
def kmp_fail(p):
2
    m = len(p)
3
    fail = [0 for i in range(m)]
4
    j,k = 1,0
5
    while j < m:
6
        if p[j] == p[k]:
7
            fail[j] = k+1
8
            j,k = j+1,k+1
9
        elif k > 0:
10
            k = fail[k-1]
11
        else:
12
            j = j+1
13
    return(fail)
14

15
def find_kmp(t, p):
16
    match =[]
17
    n,m = len(t),len(p)
18
    if m == 0:
19
        match.append(0)
20
    fail = kmp_fail(p)
21
    j = 0
22
    k = 0
23
    while j < n:
24
        if t[j] == p[k]:
25
            if k == m - 1:
26
                match.append(j - m + 1)
27
                k = 0
28
                j = j - m + 2
29
            else:
30
                j,k = j+1,k+1
31
        elif k > 0:
32
            k = fail[k-1]
33
        else:
34
            j = j+1
35
    return(match)
36
print(find_kmp('ababaabbaba','aba'))

Output

xxxxxxxxxx
1
1
[0, 2, 8]

Analysis

• The Knuth, Morris, Pratt algorithm efficiently computes the automaton describing prefix matches in the pattern p

• Complexity of preprocessing the fail function is $O(m)$$O(m)$

• After preprocessing, can check matches in the text t in $O(n)$$O(n)$

• Overall, KMP algorithm works in time $O(m+n)$$O(m + n)$

 

Tries

• A trie is a special kind of tree

  • From “information retrieval”

  • Pronounced try, distinguish from tree

• Rooted tree

  • Other than root, each node labelled by a letter from Σ

  • Children of a node have distinct labels

• Each maximal path is a word

  • One word should not be a prefix of another

  • Add special end of word symbol $

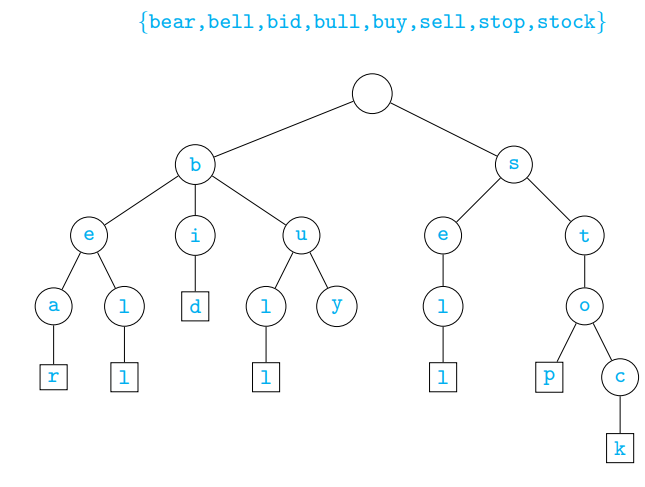
• Build a trie T from a set of words S with s words and n total symbols

• To search for a word w, follow its path

  • If the node we reach has $ as a successor represent $w\in S$$w\in S$

  • $w\notin S-$$w\not\in S-$ if path cannot be completed, or w is a prefix of some $w^{‘}\in S$$w^`\in S$

• Build a trie T from a set of words S with s words and n total symbols

• Basic properties for T built from S

  • Height of T is $ma{x}_{w\in S}len(w)$$max_{w∈S} len(w)$

  • A node has at most |Σ| children

  • The number of leaves in T is s

  • The number of nodes in T is n + 1, plus s nodes labelled $

Implementation of Tries

xxxxxxxxxx
31
1
class Trie:
2
    def __init__(self,S=[]):
3
        self.root = {}
4
        for s in S:
5
            self.add(s)
6
    def add(self,s):
7
        curr = self.root
8
        s = s + "$"
9
        for c in s:
10
            if c not in curr.keys():
11
                curr[c] = {}
12
            curr = curr[c]
13
    def query(self,s):
14
        curr = self.root
15
        for c in s:
16
            if c not in curr.keys():
17
                return(False)
18
            curr = curr[c]
19
        if "$" in curr.keys():
20
            return(True)
21
        else:
22
            return(False)
23
        
24
T = Trie()
25
T.add('car')
26
T.add('card')
27
T.add('care')
28
T.add('dog')
29
T.add('done')
30
print(T.query('dog'))
31
print(T.query('cat'))

Output

xxxxxxxxxx
2
1
True
2
False

Analysis

• Tries are useful to preprocess fixed text for multiple searches

• Searching for p is proportional to length of p

• Main drawback of a trie is size

 

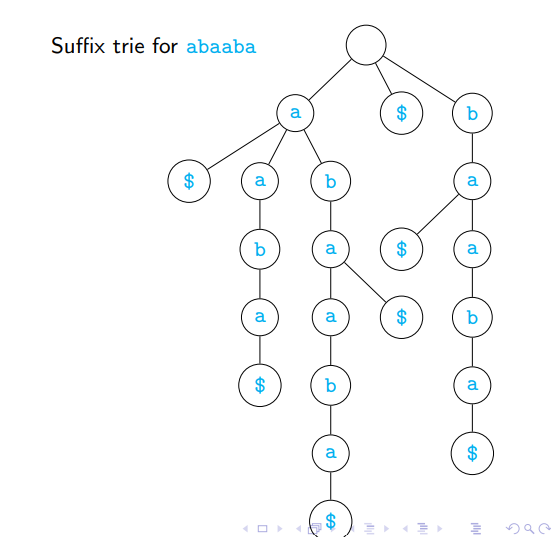
Suffix Tries

• Expand S to include all suffixes

  • For simplicity, assume S = {s}

  • suffix(S) = {w | ∃v, vw = s}

• Build a trie for suffix(S)

  • Use $ to mark end of word

  • Suffix trie for S

• Using a suffix trie we can answer the following

  • Is w a substring of s?

  • How many times does w occur as a substring in s ?

  • What is the longest repeated substring in s ?

Implementation of suffix tries

xxxxxxxxxx
24
1
class SuffixTrie:
2
    def __init__(self,s):
3
        self.root = {}
4
        s = s + "$"
5
        for i in range(len(s)):
6
            curr = self.root
7
            for c in s[i:]:
8
                if c not in curr.keys():
9
                    curr[c] = {}
10
                curr = curr[c]
11
    def followPath(self,s):
12
        curr = self.root
13
        for c in s:
14
            if c not in curr.keys():
15
                return(None)
16
            curr = curr[c]
17
        return(curr)
18
    def hasSuffix(self,s):
19
        node = self.followPath(s)
20
        return(node is not None and "$" in node.keys())
21
ST = SuffixTrie('card')
22
print(ST.root)
23
print(ST.followPath('a'))
24
print(ST.hasSuffix('aa'))

Output

xxxxxxxxxx
2
1
{'r': {'d': {'$': {}}}}
2
False

 

Regular expression

use lecture's slides