
Home Week-8 Week-10
PDSA - Week 9
PDSA - Week 9Dynamic programming Dynamic programming problemsGrid pathsLongest Common Sub Word (LCW)Longest Common Sub Sequence (LCS)Edit distanceMatrix multiplication
Dynamic programming
Solution to original problem can be derived by combining solutions to subproblems
Examples: Factorial, Insertion sort, Fibonacci series
Anticipate the structure of subproblems
Derive from inductive definition
Solve subproblems in topological order
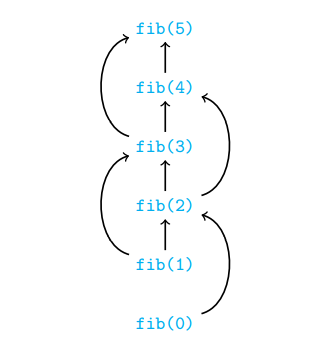
Memoization
Inductive solution generates same subproblem at different stages
Naïve recursive implementation evaluates each instance of subproblem from scratch
Build a table of values already computed – Memory table
Store each newly computed value in a table
Look up the table before making a recursive call
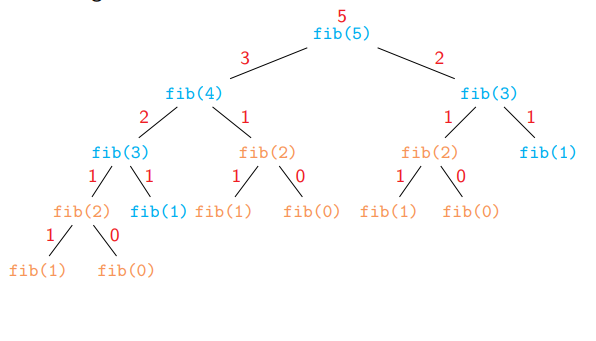
Example of
Simple recursive
1def fibrec(n):2 if n <= 1:3 return n 4 return fibrec(n - 1) + fibrec(n - 2)
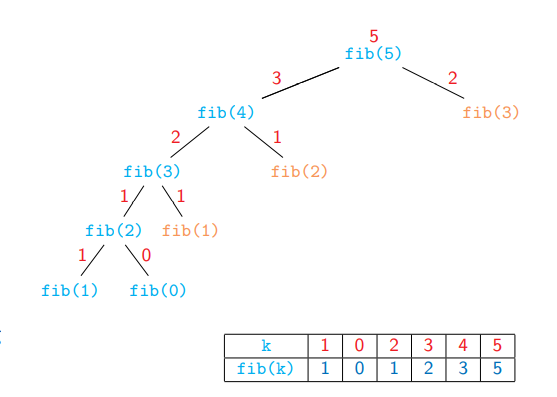
Memoization
xxxxxxxxxx71memo ={}2def fib(n):3 if n <= 1:4 memo[n] = n5 if n not in memo:6 memo[n] = fib(n-1) + fib(n-2)7 return memo[n]
Dynamic programming
xxxxxxxxxx61def fib(n):2 T = [0] * (n + 1)3 T[1] = 14 for i in range(2, n + 1):5 T[i] = T[i - 1] + T[i - 2]6 return T[n]
Comparison
x1#simple recursive2def fibrec(n):3 if n <= 1:4 return n 5 return fibrec(n - 1) + fibrec(n - 2)6
7# memoization topdown8memo ={}9def fibmem(n):10 if n <= 1:11 memo[n] = n12 if n not in memo:13 memo[n] = fibmem(n-1) + fibmem(n-2)14 return memo[n]15
16# DP tabulation bottom up17def fibtab(n):18 T = [0] * (n + 1)19 T[1] = 120 for i in range(2, n + 1):21 T[i] = T[i - 1] + T[i - 2]22 return T[n]23
24
25n=int(input())26import time27t1 = time.perf_counter()28res1 = fibrec(n)29ft1 = time.perf_counter() - t130
31t1 = time.perf_counter()32res2 = fibmem(n)33ft2 = time.perf_counter() - t134
35t1 = time.perf_counter()36res3 = fibtab(n)37ft3 = time.perf_counter() - t138
39print(res1,ft1)40print(res2,ft2)41print(res3,ft3)
Dynamic programming problems
Grid paths
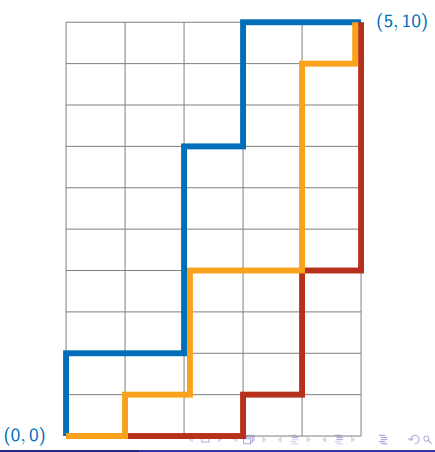
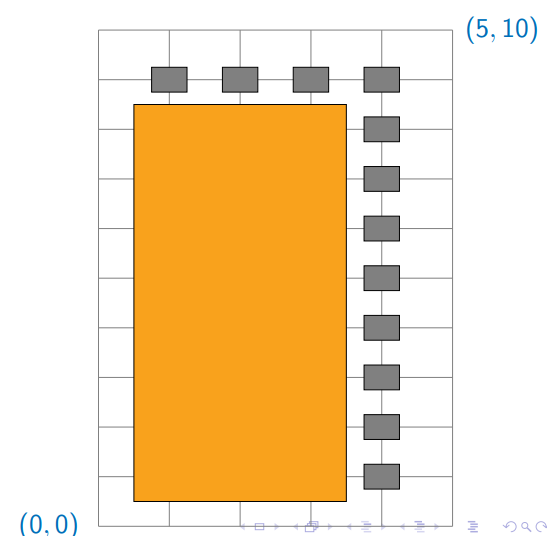
Rectangular grid of one-way roads
Can only go up and right
How many paths from (0, 0) to
Every path has
What if an intersection is blocked?
Need to discard paths passing through blocked intersection
Inductive structure

Fill the grid by row, column or diagonal

Memoization vs dynamic programming
Barrier of holes just inside the border
Memoization never explores the shaded region
Memo table has O(m + n) entries
Dynamic programming blindly fills all mn cells of the table
Tradeoff between recursion and iteration
“Wasteful” dynamic programming still better in general
Complexity is
Implementation for Grid Path problem:
Simple recursive
x
171def grid_rec(x,y,barrier):2 global count3 count+=14 if x < 1 or y < 1:5 return 16 elif (x,y) in barrier:7 return 0 8 else:9 return grid_rec(x-1,y,barrier) + grid_rec(x,y-1,barrier)10 11
12count = 013barrier = [(1,9),(2,9),(3,9),(4,9),(4,8),(4,7),(4,6),(4,5),(4,4),(4,3),(4,2),(4,1)]14print("Total path= ",grid_rec(5,10,barrier))15print("recursive call count= ",count)
Memoization
x
231def grid_memo(x,y):2 global count3 count+=14 if (x,y) in memo_table:5 return memo_table[(x,y)]6 else:7 memo_table[(x,y)] = grid_memo(x-1,y) + grid_memo(x,y-1)8 return memo_table[(x,y)]9
10
11count = 012memo_table = {}13for i in range(6):14 memo_table[(i,0)]=115for i in range(11):16 memo_table[(0,i)]=117barrier = [(1,9),(2,9),(3,9),(4,9),(4,8),(4,7),(4,6),(4,5),(4,4),(4,3),(4,2),(4,1)]18
19for k in barrier:20 if (k[0],k[1]) not in memo_table.keys():21 memo_table[(k[0],k[1])] = 022print("Total path= ",grid_memo(5,10))23print("recursive call count= ",count)
Dynamic programming
x
171import numpy as np2def grid_tab(x,y,barrier):3 M = np.zeros((x+1,y+1))4 for i in range(x+1):5 for j in range(y+1):6 if i == 0 or j == 0:7 M[i,j] = 18 for i in range(1,x+1):9 for j in range(1,y+1):10 if (i,j) in barrier:11 M[i,j] = 012 else:13 M[i,j] = M[i-1,j] + M[i,j-1]14 print (M)15 return int(M[x,y])16 17
18barrier = [(1,9),(2,9),(3,9),(4,9),(4,8),(4,7),(4,6),(4,5),(4,4),(4,3),(4,2),(4,1)]19print("Total path= ",grid_tab(5,10,barrier))
Longest Common Sub Word (LCW)
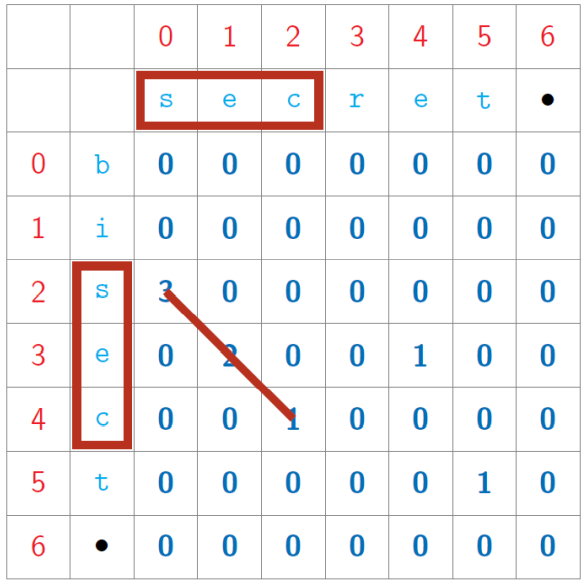
Given two strings, find the (length of the) longest common sub word
Subproblems are LCW(i, j), for 0 ≤ 𝑖 ≤ 𝑚, 0 ≤ 𝑗 ≤ 𝑛
Table of 𝑚 + 1 𝑛 + 1 values
Inductive structure
Start at bottom right and fill row by row or column by column
Implementation
xxxxxxxxxx171def LCW(s1,s2):2 import numpy as np3 (m,n) = (len(s1),len(s2))4 lcw = np.zeros((m+1,n+1))5 maxw = 06 for c in range(n-1,-1,-1):7 for r in range(m-1,-1,-1):8 if s1[r] == s2[c]:9 lcw[r,c] = 1 + lcw[r+1,c+1]10 else:11 lcw[r,c] = 012 if lcw[r,c] > maxw:13 maxw = lcw[r,c] 14 return maxw15s1 = 'bisect'16s2 = 'secret'17print(LCW(s1,s2))Output
xxxxxxxxxx113.0
Complexity
Longest Common Sub Sequence (LCS)
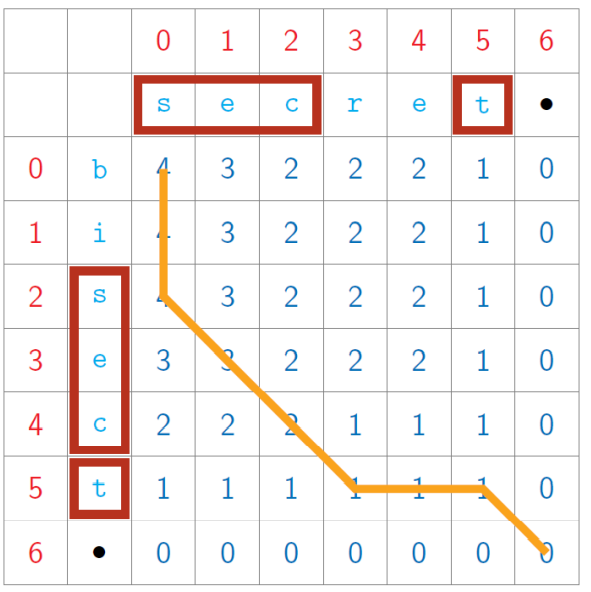
Subsequence – can drop some letters in between
Subproblems are LCS(i, j), for 0 ≤ 𝑖 ≤ 𝑚, 0 ≤ 𝑗 ≤ 𝑛
Table of 𝑚 + 1 𝑛 + 1 values
Inductive structure
Start at bottom right and fill row by row, column or diagonal
Implementation
xxxxxxxxxx141def LCS(s1,s2):2 import numpy as np3 (m,n) = (len(s1),len(s2))4 lcs = np.zeros((m+1,n+1))5 for c in range(n-1,-1,-1):6 for r in range(m-1,-1,-1):7 if s1[r] == s2[c]:8 lcs[r,c] = 1 + lcs[r+1,c+1]9 else:10 lcs[r,c] = max(lcs[r+1,c], lcs[r,c+1]) 11 return lcs[0,0]12s1 = 'secret'13s2 = 'bisect'14print(LCS(s1,s2))Output
xxxxxxxxxx114.0
Complexity
Edit distance
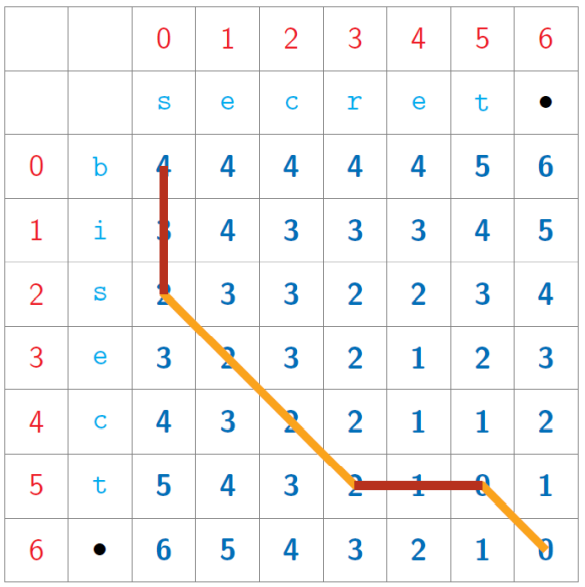
Minimum number of editing operations needed to transform one document to the other
Subproblems are ED(i, j), for 0 ≤ 𝑖 ≤ 𝑚, 0 ≤ 𝑗 ≤ 𝑛
Table of 𝑚 + 1 𝑛 + 1 values ▪
Inductive structure
Start at bottom right and fill row, column or diagonal
Implementation
xxxxxxxxxx161def ED(u,v):2 import numpy as np3 (m,n) = (len(u),len(v))4 ed = np.zeros((m+1,n+1))5 for i in range(m-1,-1,-1):6 ed[i,n] = m-i7 for j in range(n-1,-1,-1):8 ed[m,j] = n-j9 for j in range(n-1,-1,-1):10 for i in range(m-1,-1,-1):11 if u[i] == v[j]:12 ed[i,j] = ed[i+1,j+1]13 else:14 ed[i,j] = 1 + min(ed[i+1,j+1], ed[i,j+1], ed[i+1,j])15 return(ed[0,0])16print(ED('bisect','secret'))Output
xxxxxxxxxx114.0
Complexity
Matrix multiplication
Matrix multiplication is associative
Bracketing does not change answer but can affect the complexity
Find an optimal order to compute the product
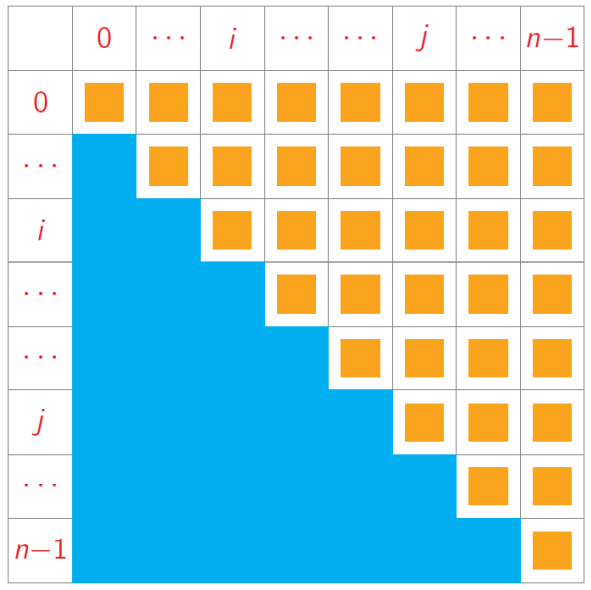
Compute C ( i, j), 0 ≤ 𝑖, 𝑗 < 𝑛, only for 𝑖 ≤ 𝑗
C ( i, j), depends on C ( i, k – 1) , C( k, j) for every 𝑖 < 𝑘 ≤ 𝑗
Diagonal entries are base case, fill matrix from main diagonal
Implementation
xxxxxxxxxx171def MM(dim):2 n = dim.shape[0]3 C = np.zeros((n,n))4 for i in range(n):5 C[i,i] = 06 for diff in range(1,n):7 for i in range(0,n-diff):8 j = i + diff9 C[i,j] = C[i,i] + C[i+1,j] + dim[i][0] * dim[i+1][0] * dim[j][1]10 print(C)11 for k in range(i+1, j+1):12 C[i,j] = min(C[i,j],C[i,k-1] + C[k,j] + dim[i][0] * dim[k][0] * dim[j][1])13 print(C)14 return(C[0,n-1])15import numpy as np16a = np.array([[2,3],[3,4],[4,5]])17print(MM(a))Output
xxxxxxxxxx1164
Complexity
Other implementation
Inductive structure
xxxxxxxxxx171def MM(dim):2 n = len(dim)3 C = []4 for i in range(n):5 L = []6 L=[0]*n7 C.append(L.copy()) 8 for diff in range(1,n):9 for i in range(0,n-diff):10 j = i + diff11 KL = []12 for k in range(i, j):13 KL.append(C[i][k] + C[k+1][j] + dim[i][0] * dim[k][1] * dim[j][1])14 C[i][j] = min(KL)15 return(C[0][n-1])16a = [[4,10],[10,3],[3,12],[12,20],[20,7]]17print(MM(a))Output
xxxxxxxxxx111344Complexity
Example
For example, we have matrices {M0, M1, M2, M3, M4} and the dimensions list of the given matrices is [[4,10],[10,3],[3,12],[12,20],[20,7]].
Matrix C : -
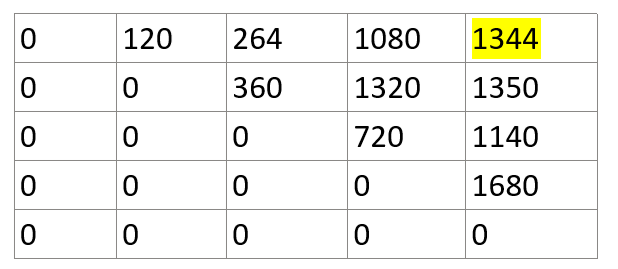
Here 1344 value is representing minimum number of multiplication steps.
We can identify the order of multiplication of matrix by storing the k value(value of k for which we get minimum steps) in matrix with steps.
Matrix C : -
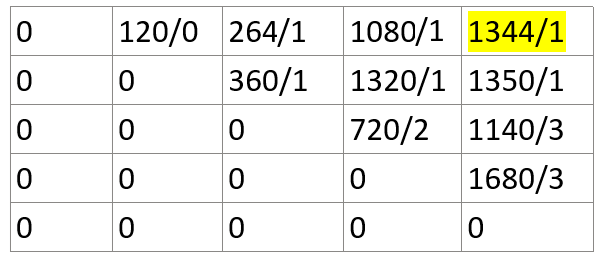
So initially we have matrices {M0, M1, M2, M3, M4} and at a time 2 matrices we can multiply.
We will check the k value for C[0][4] which is 1, so we can parenthesize the order like{(M0 M1)(M2 M3 M4)} now we have to check the order in the second bracket matrix M2, M3, M4, so we will check the value C[2][4] which is 3 then we can parenthesize the order like ((M2 M3) M4) So, the final order will be (M0 M1)((M2 M3) M4).