---

Home Week-6 Week-8

---

 

PDSA - Week 7

Balanced search tree (AVL Tree)

Binary search tree

• find(), insert() and delete() all walk down a single path
• Worst-case: height of the tree An unbalanced tree with n nodes may have height $O(n)$$O(n)$

AVL Tree

• Balanced trees have height $O(logn)$$O(log n)$
• Using rotations, we can maintain height balance
• Height balanced trees have height $O(logn)$$O(log n)$
• find(), insert() and delete() all walk down a single path, take time $O(logn)$$O(log n)$
• Minimum number of node $S(h)=S(h-2)+S(h-1)+1$$S(h) = S(h-2) + S(h-1) + 1$
• Maximum number of nodes $2^h-1$$2^h - 1$

Example for creation of AVL Tree

 

Implementation

x
1
class AVLTree:
2
    # Constructor:
3
    def __init__(self,initval=None):
4
        self.value = initval
5
        if self.value:
6
            self.left = AVLTree()
7
            self.right = AVLTree()
8
            self.height = 1
9
        else:
10
            self.left = None
11
            self.right = None
12
            self.height = 0
13
        return
14

15
    def isempty(self):
16
        return (self.value == None)
17

18
    def isleaf(self):
19
        return (self.value != None and self.left.isempty() and self.right.isempty())
20

21
    def leftrotate(self):
22
        v = self.value
23
        vr = self.right.value
24
        tl = self.left
25
        trl = self.right.left
26
        trr = self.right.right
27
        newleft = AVLTree(v)
28
        newleft.left = tl
29
        newleft.right = trl
30
        self.value = vr
31
        self.right = trr
32
        self.left = newleft
33
        return
34

35
    def rightrotate(self):
36
        v = self.value
37
        vl = self.left.value
38
        tll = self.left.left
39
        tlr = self.left.right
40
        tr = self.right
41
        newright = AVLTree(v)
42
        newright.left = tlr
43
        newright.right = tr
44
        self.right = newright
45
        self.value = vl
46
        self.left = tll
47
        return
48

49

50
    def insert(self,v):
51
        if self.isempty():
52
            self.value = v
53
            self.left = AVLTree()
54
            self.right = AVLTree()
55
            self.height = 1
56
            return        
57
        if self.value == v:
58
            return        
59
        if v < self.value:
60
            self.left.insert(v)
61
            self.rebalance()
62
            self.height = 1 + max(self.left.height, self.right.height)            
63
        if v > self.value:
64
            self.right.insert(v)
65
            self.rebalance()            
66
            self.height = 1 + max(self.left.height, self.right.height)    
67
                              
68
    def rebalance(self):
69
        if self.left == None:
70
            hl = 0
71
        else:
72
            hl = self.left.height
73
        if self.right == None:
74
            hr = 0
75
        else:
76
            hr = self.right.height                        
77
        if  hl - hr > 1:
78
            if self.left.left.height > self.left.right.height:
79
                self.rightrotate()
80
            if self.left.left.height < self.left.right.height:
81
                self.left.leftrotate()
82
                self.rightrotate()
83
            self.updateheight()        
84
        if  hl - hr < -1:
85
            if self.right.left.height < self.right.right.height:
86
                self.leftrotate()
87
            if self.right.left.height > self.right.right.height:
88
                self.right.rightrotate()
89
                self.leftrotate()
90
            self.updateheight()
91
            
92
    def updateheight(self):
93
        if self.isempty():
94
            return
95
        else:
96
            self.left.updateheight()
97
            self.right.updateheight()
98
            self.height = 1 + max(self.left.height, self.right.height)       
99
   
100
        
101
    def inorder(self):
102
        if self.isempty():
103
            return([])
104
        else:
105
            return(self.left.inorder()+ [self.value]+ self.right.inorder())
106
    def preorder(self):
107
        if self.isempty():
108
            return([])
109
        else:
110
            return([self.value] + self.left.preorder()+  self.right.preorder())
111
    def postorder(self):
112
        if self.isempty():
113
            return([])
114
        else:
115
            return(self.left.postorder()+ self.right.postorder() + [self.value])
116

117
A = AVLTree()
118
nodes = eval(input())
119
for i in nodes:
120
    A.insert(i)
121

122
print(A.inorder())
123
print(A.preorder())
124
print(A.postorder())

Sample Input

xxxxxxxxxx
1
1
[1,2,3,4,5,6,7] #order of insertion

Output

xxxxxxxxxx
3
1
[1, 2, 3, 4, 5, 6, 7] #inorder traversal
2
[4, 2, 1, 3, 6, 5, 7] #preorder traversal
3
[1, 3, 2, 5, 7, 6, 4] #postorder traveral

 

 

Greedy Algorithm

• Need to make a sequence of choices to achieve a global optimum

• At each stage, make the next choice based on some local criterion

• Never go back and revise an earlier decision

• Drastically reduces space to search for solutions

• Greedy strategy needs a proof of optimality

• Example :

  • Dijkstra's
  • Prim's
  • Kruskal's
  • Interval scheduling
  • Minimize lateness
  • Huffman coding

 

Interval scheduling

Scenario example

▪ IIT Madras has a special video classroom for delivering online lectures

▪ Different teachers want to book the classroom

▪ Slots may overlap, so not all bookings can be honored

▪ Choose a subset of bookings to maximize the number of teachers who get to use the room

 

Algorithm

1. Sort all jobs which based on end time in increasing order.
2. Take the interval which has earliest finish time.
3. Repeat next two steps till you process all jobs.
4. Eliminate all intervals which have start time less than selected interval’s end time.
5. If interval has start time greater than current interval’s end time, at it to set. Set current interval to new interval.

 

Implementation

xxxxxxxxxx
21
1
def tuplesort(L, index):
2
    L_ = []
3
    for t in L:
4
        L_.append(t[index:index+1] + t[:index] + t[index+1:])
5
    L_.sort()
6

7
    L__ = []
8
    for t in L_:
9
        L__.append(t[1:index+1] + t[0:1] + t[index+1:])
10
    return L__
11

12
def intervalschedule(L):
13
    sortedL = tuplesort(L, 2)
14
    accepted = [sortedL[0][0]]
15
    for i, s, f in sortedL[1:]:
16
        if s > L[accepted[-1]][2]:
17
            accepted.append(i)
18
    return accepted
19
#(job id,start time, finish time) in each tuple of list L
20
L = [(0, 1, 2),(1, 1, 3),(2, 1, 5),(3, 3, 4),(4, 4, 5),(5, 5, 8),(6, 7, 9),(7, 10, 13),(8, 11, 12)]
21
print(len(intervalschedule(L)))

Output

xxxxxxxxxx
1
1
4

Analysis

• Initially, sort n bookings by finish time — $O(nlogn)$$O(n log n)$
• Single scan, $O(n)$$O(n)$
• overall $O(nlogn)$$O(n log n)$

 

Example

In the table below, we have 8 activities with the corresponding start and finish times, It might not be possible to complete all the activities since their time frame can conflict. For example, if any activity starts at time 0 and finishes at time 4, then other activities can not start before 4. It can be started at 4 or afterwards.

What is the maximum number of activities which can be performed without conflict?

Activity	Start time	Finish time
A	1	2
B	3	4
C	0	6
D	1	4
E	4	5
F	5	9
G	9	11
H	8	10

Answer

5

 

 

Minimize lateness

Scenario example

▪ IIT Madras has a single 3D printer

▪ A number of users need to use this printer

▪ Each user will get access to the printer, but may not finish before deadline

▪ Goal is to minimize the lateness

Algorithm

1. Sort all job in ascending order of deadlines

2. Start with time t = 0

3. For each job in the list

   1. Schedule the job at time t
   2. Finish time = t + processing time of job
   3. t = finish time

4. Return (start time, finish time) for each job

 

Implementation

xxxxxxxxxx
26
1
from operator import itemgetter
2
 
3
def minimize_lateness(jobs):
4
    schedule =[]
5
    max_lateness = 0
6
    t = 0
7
     
8
    sorted_jobs = sorted(jobs,key=itemgetter(2))
9
     
10
    for job in sorted_jobs:
11
        job_start_time = t
12
        job_finish_time = t + job[1]
13
 
14
        t = job_finish_time
15
        if(job_finish_time > job[2]):
16
            max_lateness =  max (max_lateness, (job_finish_time - job[2]))
17
        schedule.append((job[0],job_start_time, job_finish_time))
18
 
19
    return max_lateness, schedule
20
 
21
jobs = [(1, 3, 6), (2, 2, 9), (3, 1, 8), (4, 4, 9), (5, 3, 14), (6, 2, 15)]
22
max_lateness, sc = minimize_lateness(jobs)
23
print ("Maximum lateness is :" + str(max_lateness))
24
for t in sc:
25
    print ('JobId= {0}, start time= {1}, finish time= {2}'.format(t[0],t[1],t[2]))
26

Output

xxxxxxxxxx
7
1
Maximum lateness is :1
2
JobId= 1, start time= 0, finish time= 3
3
JobId= 3, start time= 3, finish time= 4
4
JobId= 2, start time= 4, finish time= 6
5
JobId= 4, start time= 6, finish time= 10
6
JobId= 5, start time= 10, finish time= 13
7
JobId= 6, start time= 13, finish time= 15

Analysis

• Sort the requests by D(i) — $O(nlogn)$$O(n log n)$
• Read all schedule in sorted order — $O(n)$$O(n)$
• overall $O(nlogn)$$O(n log n)$

 

 

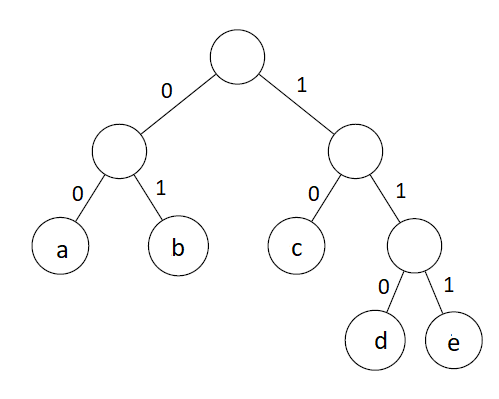
Huffman Algorithm

Algorithm

1. Calculate the frequency of each character in the string.
2. Sort the characters in increasing order of the frequency.
3. Make each unique character as a leaf node.
4. Create an empty node z. Assign the minimum frequency to the left child of z and assign the second minimum frequency to the right child of z. Set the value of the z as the sum of the above two minimum frequencies.
5. Remove these two minimum frequencies from Q and add the sum into the list of frequencies.
6. Insert node z into the tree.
7. Repeat steps 3 to 5 for all the characters.
8. For each non-leaf node, assign 0 to the left edge and 1 to the right edge.

 

Example

Implementation

xxxxxxxxxx
48
1

2
class Node:
3
    def __init__(self,frequency,symbol = None,left = None,right = None):
4
        self.frequency = frequency
5
        self.symbol = symbol
6
        self.left = left
7
        self.right = right
8

9
# Solution        
10
        
11
def Huffman(s):
12
    huffcode = {}
13
    char = list(s)
14
    freqlist = []
15
    unique_char = set(char)
16
    for c in unique_char:
17
        freqlist.append((char.count(c),c))
18
    nodes = []
19
    for nd in sorted(freqlist):
20
        nodes.append((nd,Node(nd[0],nd[1])))
21
    while len(nodes) > 1:
22
        nodes.sort()
23
        L = nodes[0][1]
24
        R = nodes[1][1]
25
        newnode = Node(L.frequency + R.frequency, L.symbol + R.symbol,L,R)
26
        nodes.pop(0)
27
        nodes.pop(0)
28
        nodes.append(((L.frequency + R.frequency, L.symbol + R.symbol),newnode))
29

30
    for ch in unique_char:
31
        temp = newnode
32
        code = ''
33
        while ch != temp.symbol:           
34
            if ch in temp.left.symbol:
35
                code += '0'
36
                temp = temp.left
37
            else:
38
                code += '1'
39
                temp = temp.right
40
        huffcode[ch] = code   
41
    return huffcode
42

43

44

45
s = 'abbcaaaabbcdddeee'
46
res = Huffman(s)
47
for char in sorted(res):
48
    print(char,res[char])

Output

xxxxxxxxxx
5
1
a 10
2
b 01
3
c 110
4
d 111
5
e 00

 

Huffman Implementation using Min Heap

Contribute by:- Jivitesh Sabharwal

xxxxxxxxxx
93
1
class min_heap:
2
    def __init__(self,nodes):
3
        self.nodes = nodes
4
        self.size =len(nodes)
5
        self.create_min_heap()
6
    
7
    def isempty(self):
8
        return len(self.nodes) == 0
9
    
10
    def min_heapify(self,s):
11
        l = 2*s + 1
12
        r = 2*s + 2
13
        small = s
14
        if l<self.size and self.nodes[l][0][0] < self.nodes[small][0][0]:
15
            small = l
16
        if r<self.size and self.nodes[r][0][0] < self.nodes[small][0][0]:
17
            small = r
18
        if small != s:
19
            self.nodes[small],self.nodes[s] = self.nodes[s],self.nodes[small]
20
            self.min_heapify(small)
21

22
    def create_min_heap(self):
23
        for i in range((self.size//2)-1,-1,-1):
24
            self.min_heapify(i)
25
    
26
    def insert_min(self,v):
27
        self.nodes.append(v)
28
        self.size += 1
29
        index = self.size -1
30
        while(index > 0):
31
            parent = (index-1)//2
32
            if self.nodes[parent][0][0] > self.nodes[index][0][0]:
33
                self.nodes[parent],self.nodes[index] = self.nodes[index],self.nodes[parent]
34
                index = parent
35
            else:
36
                break
37
        pass
38
    
39
    def del_minheap(self):
40
        item = None
41
        if self.isempty():
42
            return item
43
        self.nodes[0],self.nodes[-1] = self.nodes[-1],self.nodes[0]
44
        item = self.nodes.pop()
45
        self.size -= 1
46
        self.min_heapify(0)
47
        return item
48

49
class Node:
50
    def __init__(self,frequency,symbol = None,left = None,right=None):
51
        self.frequency = frequency
52
        self.symbol = symbol
53
        self.left = left
54
        self.right = right
55

56
def Huffman(s):
57
    freqlist = []
58
    huffcode = {}
59
    char = list(s)
60
    unique_char = set(char)
61
    for c in unique_char:
62
        freqlist.append((char.count(c),c))
63
    nodes = []
64
    for nd in sorted(freqlist):
65
        nodes.append((nd,(Node(nd[0],nd[1]))))
66
    minheap_nodes = min_heap(nodes)
67

68
    while(minheap_nodes.size > 1):
69
        
70
        L = minheap_nodes.del_minheap()[1]
71
        R = minheap_nodes.del_minheap()[1]
72
        newnode = Node(L.frequency+R.frequency,L.symbol+R.symbol,L,R)
73
        internal_node = tuple(((L.frequency+R.frequency,L.symbol+R.symbol),newnode))
74
        minheap_nodes.insert_min(internal_node)
75

76
    for ch in unique_char:
77
        temp = newnode
78
        code = ''
79
        while ch!=temp.symbol:
80
            if ch in temp.left.symbol:
81
                code += '0'
82
                temp = temp.left
83
            else:
84
                code+= '1'
85
                temp = temp.right
86
        huffcode[ch] = code
87
    return huffcode 
88

89

90
s = 'abbcaaaabbcdddeee'
91
res = Huffman(s)
92
for char in sorted(res):
93
    print(char,res[char])

Output

xxxxxxxxxx
5
1
a 10
2
b 01
3
c 110
4
d 111
5
e 00

 

Analysis

• At each recursive step, extract letters with minimum frequency and replace by composite letter with combined frequency
• Store frequencies in an array
• Linear scan to find minimum values
• $|𝐴|=𝑘$$|𝐴| = 𝑘$, number of recursive calls is $k–1$$k – 1$
• Complexity is $𝑂({𝑘}^2)$$𝑂(𝑘^2 )$
• Instead, maintain frequencies in an heap
• Extracting two minimum frequency letters and adding back compound letter are both $𝑂(log𝑘)$$𝑂(log 𝑘)$
• Complexity drops to $𝑂(klog𝑘)$$𝑂(k log 𝑘)$