---

Home Week-7 Week-9

---

 

PDSA - Week 8

Divide and conquer

• Break up a problem into disjoint subproblems

• Combine these subproblem solutions efficiently

• Examples

  • Merge sort

    • Split into left and right half and sort each half separately
    • Merge the sorted halves

  • Quicksort

    • Rearrange into lower and upper partitions, sort each partition separately
    • Place pivot between sorted lower and upper partitions

 

Divide and conquer example

Counting inversions

• Compare your profile with other customers

• Identify people who share your likes and dislikes

• No inversions – rankings identical

• Every pair inverted – maximally dissimilar

• Number of inversions ranges from 0 to n(n – 1) / 2

  

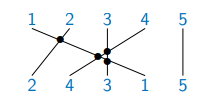
• An inversion is a pair (i, j), i < j, where j appears before i

• Recurrence: $T(n)=2T(n/2)+n=𝑂(nlog𝑛)$$T(n) = 2T(n / 2) + n = 𝑂(n log 𝑛)$

 

Implementation

​x
1
def mergeAndCount(A,B):
2
    (m,n) = (len(A),len(B))
3
    (C,i,j,k,count) = ([],0,0,0,0)
4
    while k < m+n:
5
        if i == m:
6
            C.append(B[j])
7
            j += 1
8
            k += 1
9
        elif j == n:
10
            C.append(A[i])
11
            i += 1
12
            k += 1
13
        elif A[i] < B[j]:
14
            C.append(A[i])
15
            i += 1
16
            k += 1
17
        else:
18
            C.append(B[j])
19
            j += 1
20
            k += 1
21
            count += m-i            
22
    return(C,count)
23

24
def inversionCount(A):
25
    n = len(A)
26
    if n <= 1:
27
        return(A,0)
28
    (L,countL) = inversionCount(A[:n//2])
29
    (R,countR) = inversionCount(A[n//2:])
30
    (B,countB) = mergeAndCount(L,R)
31
    return(B,countL + countR + countB)
32
L = [2,4,3,1,5]
33
print(inversionCount(L)[1])

Output

xxxxxxxxxx
1
1
4 # 4 is the number of inversions

 

Closest pair of points

• Several objects on screen

• Basic step: find closest pair of objects

• $n$$n$ objects — naive algorithm is $n^2$$n^2$

  • For each pair of objects, compute their distance
  • Report minimum distance across all pairs

• There is a clever algorithm that takes time $O(nlogn)$$O(n log n)$ using divide and conquer

• Given n points $p1,p2,...,pn$$p1, p2, . . . , pn$ find the closest pair

  • Assume no two points have same $x$$x$ or $y$$y$ coordinate
  • Split the points into two halves by vertical line
  • Recursively compute closest pair in each half
  • Compare shortest distance in each half to shortest distance across the dividing line

• Recurrence: $𝑇𝑛=2𝑇𝑛/2+𝑂(𝑛)$$𝑇 𝑛 = 2𝑇 𝑛 / 2 + 𝑂(𝑛)$

• Overall: $𝑂(𝑛log𝑛)$$𝑂(𝑛 log 𝑛)$

Pseudocode

xxxxxxxxxx
11
1
def ClosestPair(Px,Py):
2
    if len(Px) <= 3:
3
        compute pairwise distances
4
        return closest pair and distance
5
    Construct (Qx,Qy), (Rx,Ry)
6
    (q1,q2,dQ) = ClosestPair(Qx,Qy)
7
    (r1,r2,dR) = ClosestPair(Rx,Ry)
8
    Construct Sy from Qy,Ry
9
    Scan Sy, find (s1,s2,dS)
10
    return (q1,q2,dQ), (r1,r2,QR), (s1,s2,dS)
11
    #depending on which of dQ, dR, dS is minimum

Implementation

xxxxxxxxxx
60
1
import math
2

3
# Returns eucledian disatnce between points p and q
4
def distance(p, q):
5
  return math.sqrt(math.pow(p[0] - q[0],2) + math.pow(p[1] - q[1],2))
6

7
def minDistanceRec(Px, Py):
8
  s = len(Px)
9
  # Given number of points cannot be less than 2.
10
  # If only 2 or 3 points are left return the minimum distance accordingly.
11
  if (s == 2):
12
    return distance(Px[0],Px[1])
13
  elif (s == 3):
14
    return min(distance(Px[0],Px[1]), distance(Px[1],Px[2]), distance(Px[2],Px[0]))
15

16
  # For more than 3 points divide the poitns by point around median of x coordinates
17
  m = s//2
18
  Qx = Px[:m]
19
  Rx = Px[m:]
20
  xR = Rx[0][0]    # minimum x value in Rx
21
  
22
  # Construct Qy and Ry in O(n) rather from Py
23
  Qy=[]
24
  Ry=[]
25
  for p in Py:
26
    if(p[0] < xR):
27
      Qy.append(p)
28
    else:
29
      Ry.append(p)
30

31
  # Extract Sy using delta
32
  delta = min(minDistanceRec(Qx, Qy), minDistanceRec(Rx, Ry))
33
  Sy = []
34
  for p in Py:
35
    if abs(p[0]-xR) <= delta:
36
      Sy.append(p)
37
    
38
  #print(xR,delta,Sy)
39
  sizeS = len(Sy)
40
  if sizeS > 1:
41
      minS = distance(Sy[0], Sy[1])
42
      for i in range(1, sizeS-1):
43
          for j in range(i, min(i+15, sizeS-1)):
44
              minS = min(minS, distance(Sy[i], Sy[j+1]))
45
      return min(delta, minS)
46
  else:
47
      return delta
48

49
def minDistance(Points):
50
  Px = sorted(Points)
51
  Py = Points
52
  Py.sort(key=lambda x: x[-1])
53
  #print(Px,Py)
54
  return round(minDistanceRec(Px, Py), 2)
55

56

57

58
pts =  [(2, 15), (40, 5), (20, 1), (21, 14), (1,4), (3, 11)]
59
result = minDistance(pts)
60
print(result)

Output

xxxxxxxxxx
1
1
4.12

 

Integer multiplication

• Traditional method: $𝑂({𝑛}^2)$$𝑂(𝑛 ^2 )$
• Naïve divide and conquer strategy: $𝑇(𝑛)=4𝑇(𝑛/2)+𝑛=𝑂({𝑛}^2)$$𝑇(𝑛) = 4𝑇(𝑛 / 2) + 𝑛 = 𝑂(𝑛^2 )$
• Karatsuba’s algorithm: $𝑇(𝑛)=3𝑇𝑛/2+𝑛\approx 𝑂𝑛log3)$$𝑇(𝑛) = 3𝑇 𝑛 / 2 + 𝑛 ≈ 𝑂 𝑛 ~log~3)$

Implementation

xxxxxxxxxx
17
1
# here 10 represent base of input numbers x and y
2
def Fast_Multiply(x,y,n):
3
    if n == 1:
4
        return x * y
5
    else:
6
        m = n/2
7
        xh = x//10**m
8
        xl = x % (10**m)
9
        yh = y//10**m
10
        yl = y % (10**m)
11
        a = xh + xl
12
        b = yh + yl
13
        p = Fast_Multiply(xh, yh, m)
14
        q = Fast_Multiply(xl, yl, m)
15
        r = Fast_Multiply(a, b, m)
16
        return p*(10**n) + (r - q - p) * (10**(n/2)) + q 
17
print(Fast_Multiply(3456,8902,4))

Output

xxxxxxxxxx
1
1
30765312.0

 

Quick select and Fast select

• Find the ${𝑘}_{𝑡ℎ}$$𝑘_{𝑡ℎ}$ smallest value in a sequence of length $𝑘$$𝑘$
• Sort in descending order and look at position $𝑘–𝑂(𝑛log𝑛)$$𝑘~ –~ 𝑂 (𝑛 log 𝑛)$
• For any fixed $𝑘$$𝑘$, find maximum for $𝑘$$𝑘$ times – $𝑂(𝑘𝑛)$$𝑂(𝑘𝑛)$
• $𝑘=n/2$$𝑘 = n / 2$ (median) – $𝑂({𝑛}^2)$$𝑂 (𝑛^2)$
• Median of medians –$𝑂(𝑛)$$𝑂(𝑛)$
• Selection becomes $𝑂(𝑛)$$𝑂(𝑛)$ in Fast select algorithm
• Quicksort becomes $𝑂(𝑛logn)$$𝑂 (𝑛 log n)$ using MoM

Implementation

xxxxxxxxxx
23
1
def quickselect(L,l,r,k): # k-th smallest in L[l:r]
2
  if (k < 1) or (k > r-l):
3
    return(None)
4

5
  (pivot,lower,upper) = (L[l],l+1,l+1)
6
  for i in range(l+1,r):
7
    if L[i] > pivot:  # Extend upper segment
8
      upper = upper + 1
9
    else: # Exchange L[i] with start of upper segment
10
      (L[i], L[lower]) = (L[lower], L[i])
11
      (lower,upper) = (lower+1,upper+1)
12
  (L[l],L[lower-1]) = (L[lower-1],L[l]) # Move pivot
13
  lower = lower - 1
14

15
  # Recursive calls
16
  lowerlen = lower - l
17
  if k <= lowerlen:
18
    return(quickselect(L,l,lower,k))
19
  elif k == (lowerlen + 1):
20
    return(L[lower])
21
  else:
22
    return(quickselect(L,lower+1,r,k-(lowerlen+1)))
23
print(quickselect([5,3,7,2,1],0,5,2))

Output

xxxxxxxxxx
1
1
2

 

Median of Medians(MoM)

• Divide L into blocks of 5

• Find the median of each block (brute force)

• Let M be the list of block medians

• Recursively apply the process to M

• We can visualize the blocks as follows

  

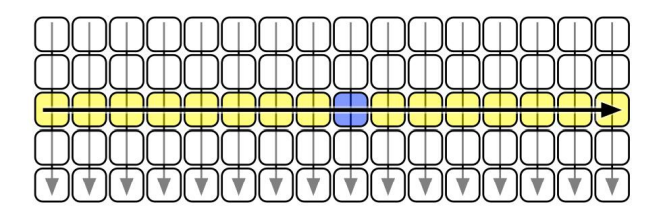
• Each block of 5 is arranged in ascending order, top to bottom

• Block medians are the middle row

• The median of block medians lies between 3len(L)/10 and 7len(L)/10

  

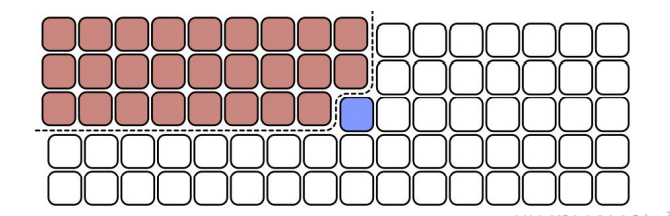
Implementation

xxxxxxxxxx
12
1
def MoM(L): # Median of medians
2
  if len(L) <= 5:
3
    L.sort()
4
    return(L[len(L)//2])
5
  # Construct list of block medians
6
  M = []
7
  for i in range(0,len(L),5):
8
    X = L[i:i+5]
9
    X.sort()
10
    M.append(X[len(X)//2])
11
  return(MoM(M))
12
print(MoM([4,3,5,6,2,1,8,9,7,10,13,15,18,17,11]))

Output

xxxxxxxxxx
1
1
8

 

Fast select using MOM

Implementation

xxxxxxxxxx
42
1
def MoM(L): # Median of medians
2
  if len(L) <= 5:
3
    L.sort()
4
    return(L[len(L)//2])
5
  # Construct list of block medians
6
  M = []
7
  for i in range(0,len(L),5):
8
    X = L[i:i+5]
9
    X.sort()
10
    M.append(X[len(X)//2])
11
  return(MoM(M))
12

13

14

15
def fastselect(L,l,r,k): # k-th smallest in L[l:r]
16
  if (k < 1) or (k > r-l):
17
    return(None)
18

19
  # Find MoM pivot and move to L[l]
20
  pivot = MoM(L[l:r])
21
  pivotpos = min([i for i in range(l,r) if L[i] == pivot])
22
  (L[l],L[pivotpos]) = (L[pivotpos],L[l])
23

24
  (pivot,lower,upper) = (L[l],l+1,l+1)
25
  for i in range(l+1,r):
26
    if L[i] > pivot:  # Extend upper segment
27
      upper = upper + 1
28
    else: # Exchange L[i] with start of upper segment
29
      (L[i], L[lower]) = (L[lower], L[i])
30
      (lower,upper) = (lower+1,upper+1)
31
  (L[l],L[lower-1]) = (L[lower-1],L[l]) # Move pivot
32
  lower = lower - 1
33
  
34
  # Recursive calls
35
  lowerlen = lower - l
36
  if k <= lowerlen:
37
    return(fastselect(L,l,lower,k))
38
  elif k == (lowerlen + 1):
39
    return(L[lower])
40
  else:
41
    return(fastselect(L,lower+1,r,k-(lowerlen+1)))
42
print(fastselect([4,3,5,6,2,1,8,9,7,10,13,15,18,17,11],0,15,4))

Output

xxxxxxxxxx
1
1
4

 

Recursion trees

• Recursion tree-Rooted tree with one node for each recursive subproblem

• Value of each node is time spent on that subproblem excluding recursive calls

• Concretely, on an input of size $n$$n$

  • $f(n)$$f (n)$ is the time spent on non-recursive work
  • $r$$r$ is the number of recursive calls
  • Each recursive call works on a subproblem of size $n/c$$n/c$

• Resulting recurrence: $T(n)=rT(n/c)+f(n)$$T(n) = rT(n/c) + f (n)$

• Root of recursion tree for $T(n)$$T(n)$ has value $f(n)$$f (n)$

• Root has $r$$r$ children, each (recursively) the root of a tree for $T(n/c)$$T(n/c)$

• Each node at level $d$$d$ has value $f(n/c^d)$$f (n/c^d )$

  • Assume, for simplicity, that $n$$n$ was a power of $c$$c$